Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 15
15. A equação
é chamada, muitas vezes, de equação de Rayleigh.
(a) Escreva a equação de Rayleigh como um sistema de duas equações de primeira ordem.
(b) Mostre que a origem é o único ponto crítico desse sistema. Determine seu tipo e se é assintoticamente estável, estável ou instável.
(c) Seja . Escolha condições iniciais e calcule a solução correspondente para o sistema em um intervalo como ou maior. Faça o gráfico de em função de e faça, também, o gráfico da trajetória no plano de fase. Observe que a trajetória tende a uma curva fechada (um ciclo limite). Estime a amplitude e o período do ciclo limite.
(d) Repita o item (c) para outros valores de , como ; ; e . Em cada caso, estime a amplitude e o período .
(e) Descreva como o ciclo limite muda quando μ aumenta. Por exemplo, faça uma tabela e/ou um gráfico de e em função de .
Passo 1
Pois bem, para começar esse problema aqui, vamos definir essa mudança aqui:
BELEZA! Com essa mudança podemos substitui na EDO
De modo que ...
Beleza, considerando agora que ...
Então podemos falar que a nossa EDO de segunda ordem pode ser escrita em termos de um sistema de EDO de primeira ordem não linear tal que:
Passo 2
Para encontramos o ou os pontos críticos, devemos igualar as derivadas a no nosso sistema:
Repare então que da primeira equação na segunda...
Isso basicamente significa de fato que o único ponto crítico .
Passo 3
Beleza! Então primeiro montemos o nosso sistema localmente linear removendo as informações de quem são e :
Agora encontremos a jacobiana disso:
Substituindo o ponto ...
Então o sistema localmente linear será...
Para provar essa questão estabilidade, vamos ter que buscar os autovalores da matriz:
Então...
Resolvendo essa equação do segundo grau...
VEJAMOS PRIMEIRO A CONDIÇÃO DE QUE
Logo, nessa condição gerará um sistema harmônico com centro em .
VEJAMOS AGORA A CONDIÇÃO DE QUE :
Nessa condição , então teremos dois autovalores imaginários com a parte real , positiva e, portanto, o sistema será instável em espiral.
VEJAMOS AGORA A CONDIÇÃO DE QUE :
Nesse caso, os valores de são reais e positivos, logo, gerará um ponto de instabilidade.
Passo 4
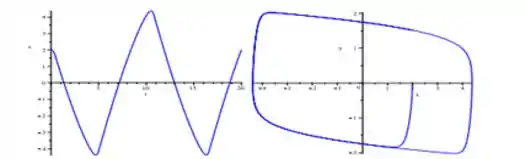
Escolhendo então e as condições iniciais e , podemos jogar em um programa de computador que nos gerará os seguintes gráficos:
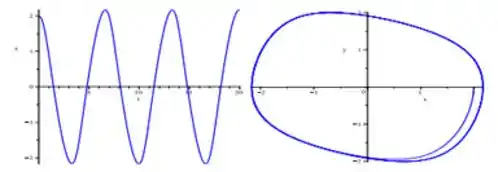
O primeiro é a plotagem de em função de e o segundo o retrato de fase. Perceba que o período nesse caso é aproximadamente .
Passo 5
Pegando as mesmas condições inicias e aplicando como pedido no exercício:
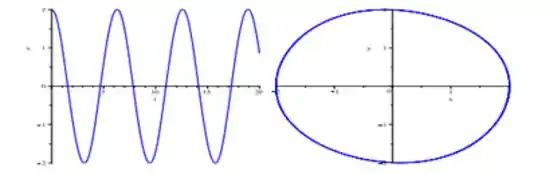
Pelo gráfico de da pra ver que e a amplitude .
PARA :
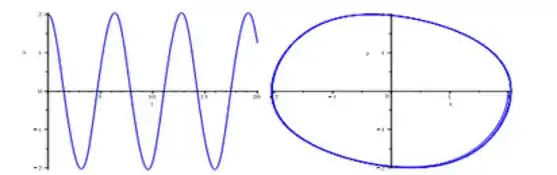
Nesse caso o valor da amplitude continua próximo de e .
PARA :
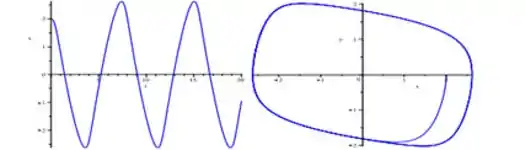
Nesse caso o valor da amplitude continua próximo de e .
PARA :
Nesse caso o valor da amplitude continua próximo de e .
Passo 6
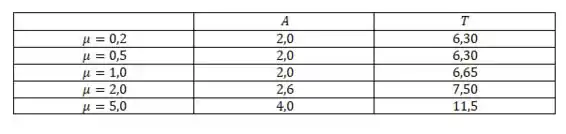
Aqui podemos reunir todas essas informações em um uma tabela pra gente ver como essas variáveis estão variando com :
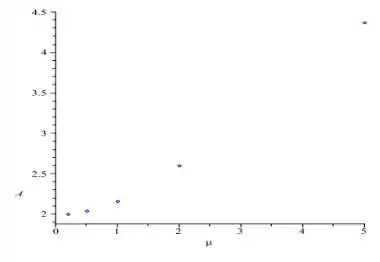
Fazendo um gráfico que reúne as informações para a amplitude...
E agora um para as informações de período:
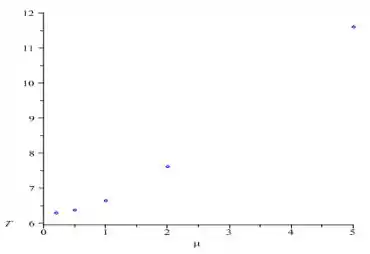
Percebemos que ambos tem um comportamento paraboloidal com a variação de , saca?
Resposta
Ei, a resposta está no passo a passo :)