Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 21

21. O sistema

x ' = 3 x + y - 1 3 x 3 - k ,                 y ' = - 1 3 x + 0,8 y - 0,7

é um caso particular das equações de Fitzhugh-Nagumo, 15 que modelam a transmissão de impulsos neurais ao longo de um axônio. O parâmetro k é o estímulo externo.

(a) Mostre que o sistema tem um único ponto crítico independente do valor de k .

(b) Encontre o ponto crítico para k   =   0 e mostre que é um ponto espiral assintoticamente estável. Repita a análise para k   =   0,5 e mostre que o ponto crítico é agora um ponto espiral instável. Desenhe um retrato de fase para o sistema em cada caso.

(c) Encontre o valor k 0 em que o ponto crítico muda de assintoticamente estável para instável. Encontre o ponto crítico e desenhe um retrato de fase para o sistema para k   =   k 0 .

(d) Para k   >   k 0 , o sistema exibe um ciclo limite assintoticamente estável; o sistema tem um ponto de bifurcação de Hopf em   k 0 . Desenhe um retrato de fase para k   =   0,4 ; 0,5 e 0,6 ; note que o ciclo limite não é pequeno quando k está perto de   k 0 . Faça também o gráfico de x em função de t e estime o período T em cada caso.

(e) Quando k aumenta mais, existe um valor k 1 no qual o ponto crítico torna-se novamente assintoticamente estável e o ciclo limite desaparece. Encontre k 1 .

Passo 1

L e t r a   A :

Bem, aqui não precisamos encontrar o ponto crítico ainda, apenas indicar que ele é único independentemente de k . Um ponto crítico sempre pode ser encontrado zerando as derivadas:

0 = 3 x + y - 1 3 x 3 - k ,                 0 = - 1 3 x + 0,8 y - 0,7

Pegando a segunda equação...

0 = x + 0,8 y - 0,7   →

E a multiplicando por - 3,75 a fim de obter - 3 y ...

0 = - 3,75 x - 3 y + 2,625

Agora podemos pegar a primeira equação...

0 = 3 x + 3 y - x 3 - 3 k

E somar as duas! Quando fizermos isso, a parte que depende de y vai desaparecer, ficando uma equação só em x :

0 = - 0,75 x - x 3 - 3 k + 2,625

Arrumando essa equação a multiplicando por - 1 ...

x 3 + 0,75 x + 3 k - 2,625 = 0

Se a gente chamar esse lado esquerdo de f x ...

f x = x 3 + 0,75 x + 3 k - 2,625

E derivar essa função...

f ' x = 3 x 2 + 0,75

Podemos perceber que ela é uma derivada estritamente positiva, o que garante ser f x uma função estritamente crescente. Como f x é uma função cúbica...

f x = x 3 + 0,75 x + 3 k - 2,625

Temos uma única solução real já que ela só é crescente! Se x então assume um único valor real, y também assumirá já que...

0 = x + 0,8 y - 0,7

y depende exclusivamente de x e de forma linear. Isso nos garante então que independente de k , teremos sempre um único ponto crítico. O seu valor sim, dependerá de k , mas não a quantidade, saca?

Passo 2

L e t r a   B :

Para k = 0 , da letra A...

x 3 + 0,75 x + 3 k - 2,625 = 0   →

x 3 + 0,75 x - 2,625 = 0

Jogando essa equação em um software de solução de equações, como o WolframAlpha, obteremos...

x ≈ 1.19941

Substituindo nessa outra equação aqui:

0 = x + 0,8 y - 0,7

Encontraremos...

y ≈ - 0,62426

O que nos dá o ponto crítico 1.19941 ,   - 0,62426 .

Quanto a análise do ponto, primeiro chamemos...

F x ,   y = 3 x + 3 y - x 3 - 3 k ,                 G x ,   y = - 1 3 x - 0,8 3 y + 0,7 3

Agora encontremos a jacobiana disso:

J x ,   y = F x F y G x G y     →

J x ,   y = 3 - 3 x 2 3 - 1 3 - 0,8 3       →

Substituindo o ponto de interesse 1.19941 ,   - 0,62426 ...

J 1.19941 ,   - 0,62426 = 3 - 3 1.19941 2 3 - 1 3 - 0,8 3     →

J 1.19941 ,   - 0,62426 = - 1,315753 3 - 1 3 - 0,8 3     →

Se calcularmos os autovalores dessa matriz usando o WolframAlpha, obteremos...

λ = - 4747259 ± i 26094,76 ⋅ 10 9 6 ⋅ 10 6

O que prova que de fato, teremos um sistema assintoticamente estável.

Passo 3

Para k = 0.5 , da letra A...

x 3 + 0,75 x + 3 k - 2,625 = 0   →

x 3 + 0,75 x - 1,125 = 0

Jogando essa equação em um software de solução de equações, como o WolframAlpha, obteremos...

x ≈ 0,804848

Substituindo nessa outra equação aqui:

0 = x + 0,8 y - 0,7

Encontraremos...

y ≈ - 0 , 13106

O que nos dá o ponto crítico 0,804848 ,   - 0,13106 .

Quanto a análise do ponto, jogando ele na Jacobiana que descobrimos...

J x ,   y = 3 - 3 x 2 3 - 1 3 - 0,8 3       →

J 0,804848 ,   - 0,13106 = 3 - 3 0,804848 2 3 - 1 3 - 0,8 3     →

J 0,804848 ,   - 0,13106 = 1,056665 3 - 1 3 - 0,8 3     →

Se calcularmos os autovalores dessa matriz usando o WolframAlpha, obteremos...

λ = 2369977 ± i 20239,28 ⋅ 10 9 6 ⋅ 10 6

O que prova que de fato, teremos um sistema instável em espiral.

Passo 4

Desenhando o retrato de fase delas usando o nosso programinha descrito no exercício 17, apenas configurando a nossa função...

x ' = 3 x + y - 1 3 x 3 - k ,                 y ' = - 1 3 x + 0,8 y - 0,7

E configurando pontos iniciais convenientes, como 1 ,   1 ...

Começando por quando k = 0 , e tomando as condições iniciais y = 1 e x = 1 , para uma dada solução (curva azul) e y = 0.5 e x = 1 , para avermelha...

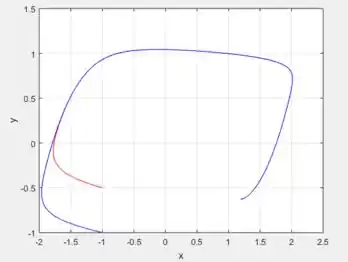
Perceba que elas param no mesmo ponto final que é justamente o nosso ponto crítico encontrado no passo 2 provando a estabilidade.

Agora em relação a segunda, considerando aqui que k = 0.5 ...

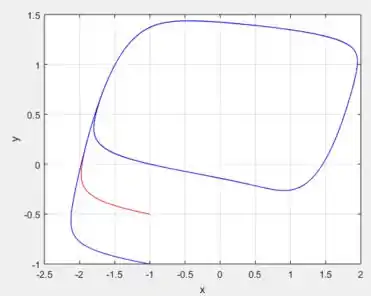
Com as mesmas condições iniciais as curvas entram em um processo ressonante, provando a instabilidade.

Passo 5

L e t r a   C :

Podemos encontrar esse valor de k , já que sabemos que o Jacobiano é dado por...

J x ,   y = 3 - 3 x 2 3 - 1 3 - 0,8 3       →

Calculando os autovalores dele então teremos...

det ⁡ 3 - 3 x 2 - r 3 - 1 3 - 0,8 3 - r = 0       →

3 - 3 x 2 - r - 0,8 3 - r + 1 = 0

Multiplicando...

- 0,8 + 0.8 x 2 + 0,8 3 r - 3 r + 3 x 2 r + r 2 + 1 = 0   →

E organizando em r (o autovalor)...

r 2 + - 8.2 3 + 3 x 2 r + 1 - 0,8 + 0.8 x 2 = 0   →

Resolvendo para r então essa equação do segundo grau (considerando x uma constante que devemos determinar)...

r = - - 8.2 3 + 3 x 2 2 ± - 8.2 3 + 3 x 2 2 - 4 1 - 0,8 + 0.8 x 2 2

Repare que o ponto limite está justamente definido pela parte real dessa equação. Se essa parte real estiver abaixo de 0 , então ela o sistema será estável, e o oposto caso ela seja maior que 0 . Logo, igualando-se a 0 ...

- 8.2 3 + 3 x 2 = 0     →

Resolvendo agora para x ...

3 x 2 = 8.2 3   →

x = ± 8.2 9   →

Vamos pegar apenas o lado positivo por enquanto e salva o negativo para o passo 6.

x = 0.954521

Beleza, então através da equação...

x 3 + 0,75 x + 3 k - 2,625 = 0   →

Podemos tirar o valor de k ...

0.954521 3 + 0,75 0.954521 + 3 k - 2,625 = 0   →

k 0 = 0.3464779

Viu só! É exatamente um ponto no interior de k = 0 e k = 0.5 , então faz sentido a nossa resposta!

Para encontrar o ponto crítico, ainda precisamos de y . Pela equação...

0 = x + 0,8 y - 0,7   →

0 = 0.954521 + 0,8 y - 0,7   →

y = - 0,31815175

Então o ponto crítico será...

0.954521 ,   - 0,31815175

Aqui está o retrato de fase considerando esse k , agora :

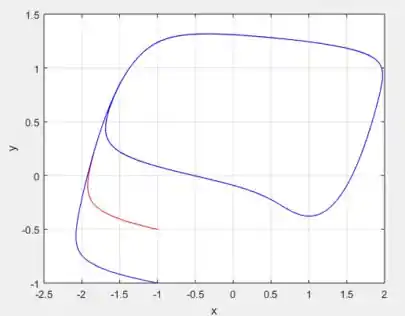
Passo 6

L e t r a   D :

Para o caso de k = 0.4 ...

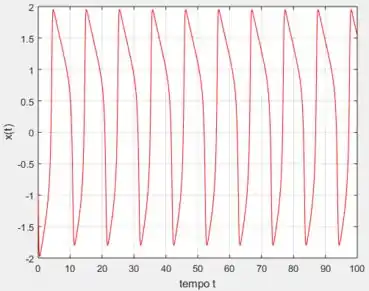
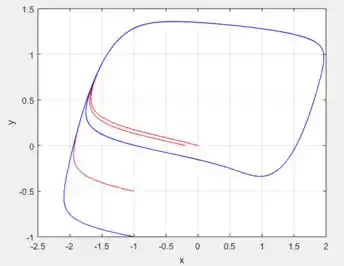
E o período, por observação é aproximadamente T = 11 .

Para k = 0.5 ...

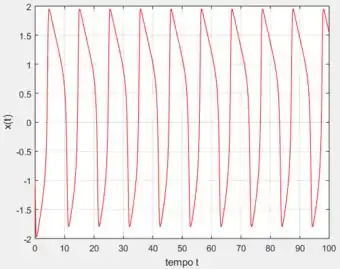
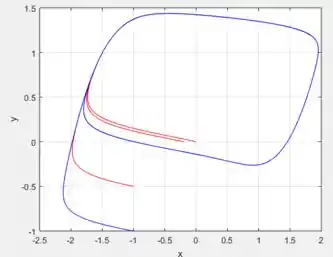
E o período T ≈ 10.5 .

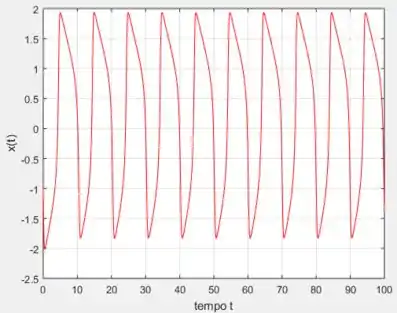
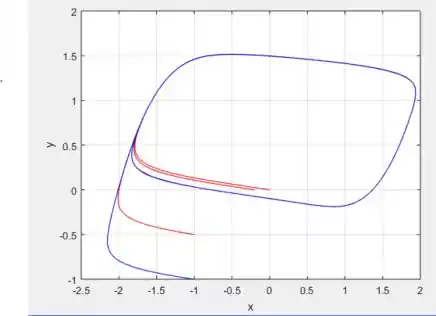
Nesse caso, observando o gráfico x × t , o período é mais ou menos T = 10 .

Passo 7

L e t r a   E :

No passos 4 , escolhemos a raiz positiva:

x = ± 8.2 9

Se escolhermos agora a raiz negativa...

x = - 0,954522

E substituindo novamente na equação do k ...

x 3 + 0,75 x + 3 k - 2,625 = 0   →

- 0,954522 3 + 0,75 - 0,954522 + 3 k - 2,625 = 0   →

k = 1.403522

Ou seja, esse corresponde ao outro ponto onde o sistema muda novamente: ele sai de instável e passa a ser estável novamente, portanto...

k 1 = 1.403522

Resposta

Letra A: Demonstração.

Letra B:

k = 0   →     1.19941 ,   - 0,62426

k = 0.5     →         0,804848 ,   - 0,13106

Letra C:

k 0 = 0.3464779

Letra D: Demonstração.

Letra E:

k 1 = 1.403522

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma generalização da equação do pêndulo não amortecido é: d 2 u d t 2 + g u = 0 Em que g 0 = 0 ,g u0 para 0uk e g u0 para - ku0 , ou seja, u g u0 para u ≠ 0 , - kuk . Note que g u = sen ⁡ u tem essa p
Em cada um dos problemas de 1 a 4, construa uma função de Liapunov adequada da forma a x 2 + c y 2 , em que a e c devem ser determinados. Depois, mostre que o ponto crítico na origem é do tipo indicad
A equação de Liénard (Problema 30 da Seção 9.3) é d 2 v d t 2 + c v . d v d t + g v = 0 Em que g satisfaz as condições do Problema 6 e c v ≥ 0 . Mostre que o ponto v = 0 , d v / d t = 0 é um ponto crí
Introduzindo variáveis adimensionais adequadas, o sistema de equações não lineares para opêndulo amortecido [Eqs. (8) da Seção 9.3] pode ser escrito na forma d x d t = y , d y d t = - y - sen ⁡ x (a)
(a) Um caso particular da equação de Liénard do Problema 8 é d 2 u d t 2 + d u d t + g u = 0 em que g satisfaz as condições do Problema 6. Fazendo x = u, y = du/dt, mostre que a origem é um ponto crít