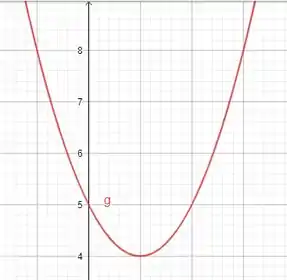
- Construir os gráficos das funções quadráticas . Dar o domínio e conjunto imagem.
Passo 1
Inicialmente vamos determinar apenas o domínio a imagem tiraremos pelo gráfico, é a forma mais fácil de se determinar a imagem!
O Domínio de uma função quadrática é sempre o conjunto dos Reais.
Passo 2
Para essa função, temos que analisar o .
Não temos raízes reais, então a função nunca corta o eixo . A função corta o eixo no ponto , tem concavidade para cima,
Cálculo do ponto de máximo:
Passo 3
Com tudo isso calculado e escrito no passo anterior, poderemos desenhar o gráfico.
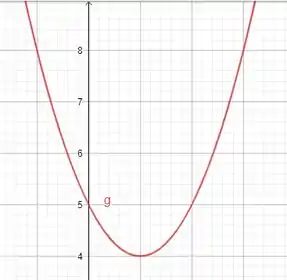
A imagem é mais simples de ser visualizada após o gráfico ter sido traçado, pois o gráfico parte de e vai indefinidamente para cima, ou seja vai de até
Resposta