Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 4
4.Construir os gráficos das racionais. Dar o domínio e conjunto imagem.
)
Passo 1
O domínio não é tão simples quanto nas anteriores, porém sabemos que nunca poderemos ter no denominador, parte de baixo da fração ! Então, para cada função vamos ter:
Para a função racional da letra , poderemos ter todos os valores dos Reais, exceto o . Escrevemos isso assim:
Para a função racional da letra , poderemos ter todos os valores dos Reais, exceto o . Escrevemos isso assim:
Para a função racional da letra , poderemos ter todos os valores dos Reais, exceto o . Escrevemos isso assim:
Desenharemos os gráficos das funções admitindo valores aleatórios de , menos os que não pertencem ao domínio
Passo 2
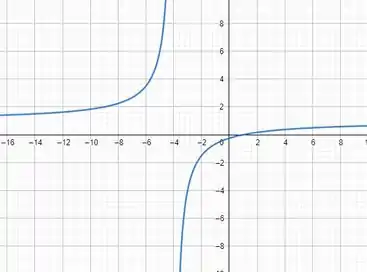
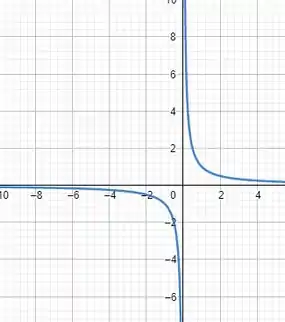
Para a primeira função faremos uma tabela de valores de a , dessa forma:
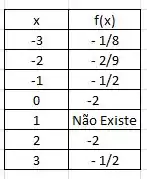
Assim poderíamos ter o esboço do gráfico e ficaria mais ou menos assim:
Do gráfico, podemos tirar a imagem também!!! Verificando quais os valores que o gráfico consegue alcançar! Todos os valores abaixo do zero, porém o próprio zero não iremos conseguir alcançar
Isso quer dizer que a imagem dessa função são os Reais negativos menos o :
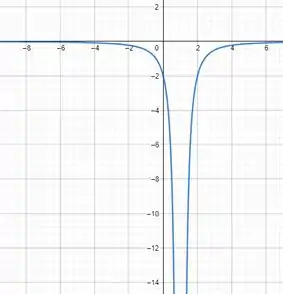
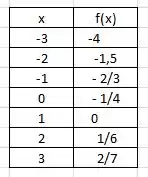
Para a função , faremos o mesmo procedimento:
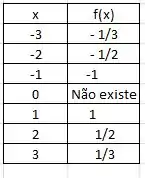
O gráfico agora ficaria mais ou menos assim.
Se seguirmos o gráfico, vamos ver que a imagem dele são todos os valores exceto o
Passo 3
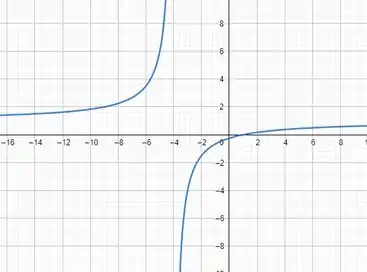
Vamos para a nossa última função!
Faremos a mesma coisa que fizemos nas anteriores valores de a .
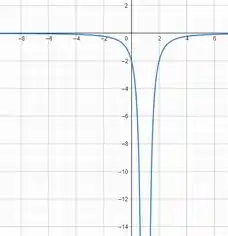
O gráfico vai ficar assim:
O único valor que o gráfico não conseguirá alcançar é o , pois se , teremos isso aqui ò:
O que é um absurdo! Então
Então a imagem é
Resposta
a)
b)
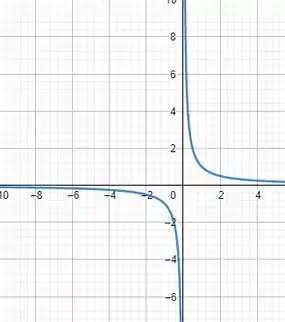
c)
