É convergente ou divergente? Justifique.
Passo 1
Devemos verificar se essa integral imprópria diverge ou converge. Neste caso, achar uma primitiva é bem complicado, de modo que vamos recorrer aos critérios de comparação!
Note que podemos escrever
Vamos olhar para a função:
Plotando para :
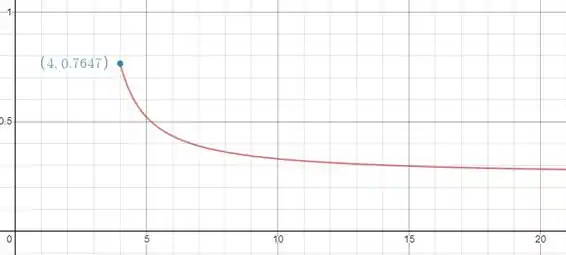
Note que , de modo que
Passo 2
Pelo teorema da página 70, temos que integrais do tipo
sempre convergem se . Neste caso, temos , de modo que a integral
é convergente.
Passo 3
Por fim, como temos que
E a integral
converge, segue pelo critério da comparação que a integral
será convergente!
Resposta
Converge.