Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 42

Convertendo em uma integral polar: Calcule a integral

∫ 0 ∞ ∫ 0 ∞ 1 1 + x 2 + y 2   d x   d y

Passo 1

Faaaala, cara! Tranquileba?

Das coordenadas polares temos que:

x = r cos ⁡ θ

y = r   s e n θ

x 2 + y 2 = r 2

E em caso de dúvidas, vejamos a figura para que possamos entender melhor.

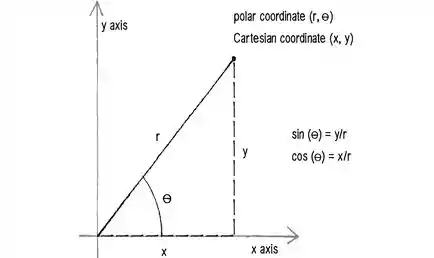
E em se tratando de integrais, quando transformamos uma integral para coordenadas polares, temos que adicionar o jacobiano das coordenadas polares, que no caso é r .

Passo 2

Dito isso, então temos:

∫ 0 π 2 ∫ 0 ∞ 1 1 + r 2   r   d r   d θ

∫ 0 π 2 ∫ 0 ∞ r 1 + r 2     d r   d θ

∫ 0 π 2 lim b → ∞ ⁡ ∫ 0 b r 1 + r 2 d r   d θ

Temos das técnicas de integração, que:

∫ x 1 + x 2 d x = 1 2 l n ⁡ ( x 2 + 1 )

Assim:

∫ 0 2 π 1 2 lim b → ∞ ⁡ ln ⁡ r 2 + 1 0 b ) d θ

1 2 lim b → ∞ ⁡ ln ⁡ r 2 + 1 0 b ) θ 0 π 2

π 4 lim b → ∞ ⁡ [ ln ⁡ r 2 + 1 0 b

π 4

Resposta

∫ 0 π 2 ∫ 0 ∞ r 1 + r 2     d r   d θ

E o valor da integral é:

π 4

Exercícios de Livros Relacionados

Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 2 1 + x 2 + y 2 d yd x
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 1 ∫ x 2 - x 2 x + 2 y d yd x
Nos Exercícios 23-26, esboce a região de integração e converta cada uma das integrais polares ou soma de integrais a uma integral cartesiana ou soma de integrais. Não calcule as integrais. ∫ 0 π 2 ∫ 0
Fórmula da área em coordenadas polares: Utilize a integral dupla em coordenadas polares para deduzir a fórmula: A = ∫ α β 1 2 r 2 d θ para a área da região em formato de leque entre a origem e a curva
Suponha que a área de uma região no plano de coordenadas polares seja A = ∫ π 4 3 4 π ∫ c o s s e c θ 2s e n θ rd rd θ Esboce a região e encontre sua área.