Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 6
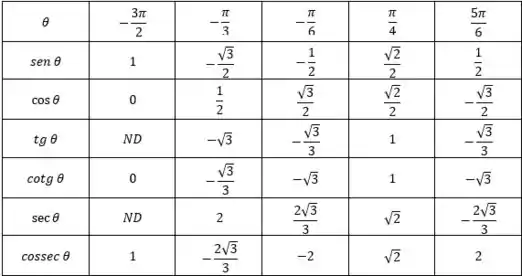
Copie e complete a tabela a seguir com valores de funções. Se a função não for definida para um dado ângulo, preencha com "ND". Não use calculadora ou tabelas.
Passo 1
Antes de começarmos a resolver, para facilitar nossos cálculos, vamos converter os ângulos que estão em radianos para graus, ok?
Como as funções , , e só dependem das outras 2 funções básicas que são e , não precisamos fazer seu cálculo diretamente. Sabendo dos valores das 2 funções básicas conseguimos descobrir seus valores.
Passo 2
Uma coisa muito importante que vale ser lembrada é que é uma função ímpar e que é uma função par, portanto também é uma função ímpar. Em outras palavras:
Uma função é uma função par se .
Uma função é uma função ímpar se .
Passo 3
Calculando os valores de , temos:
Passo 4
Calculando os valores de , temos:
Passo 5
Como é a razão entre a função seno e a função cosseno, temos que:
Passo 6
Como é a razão entre a função cosseno e a função seno, temos que:
Passo 7
Como é o inverso da função cosseno, temos que:
Passo 8
Como é o inverso da função seno, temos que:
Passo 9
Completando a tabela com os dados obtidos, teremos que a tabela ficará da seguinte forma:
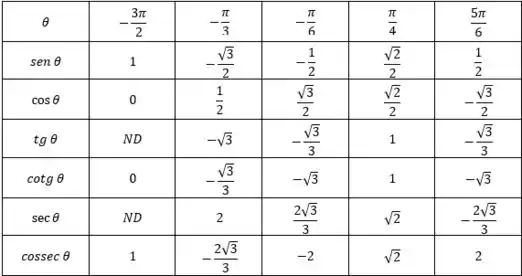
Resposta
