Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 46b

Traçar o gráfico das funções trigonométricas. Comparar cada conjunto identificando a transformação ocorrida. Identificar domínio, conjunto imagem, máximos e mínimos, crescimento e decrescimento.

  1. f x = sen ⁡ x         g x = 2 sen ⁡ x             h x = 1 2 sen ⁡ x
  2. f x = sen ⁡ x         g x = 2 sen ⁡ x             h x = sen ⁡ 1 2 x
  3. f x = cos ⁡ x         g x = cos ⁡ ( x + 3 )             h x = cos ⁡ ( x - 3 )

Passo 1

Galerinha, para otimizar a visualização, vamos traçar os três gráficos no mesmo sistema de eixo.

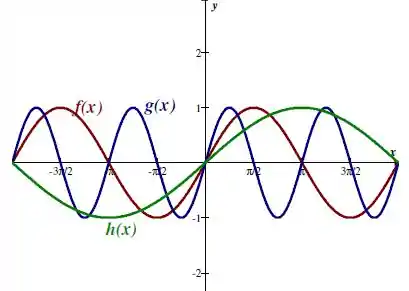
  • Nesse caso, as três funções tem o mesmo domínio.
  • As imagens aqui são: I m f = I m g = I m h = - 1,1
  • Pontos de máximo

f x = π 2 + 2 k π ,   k ∈ Z

g x = π 4 + k π ,   k ∈ Z

h x = π + 4 k π ,   k ∈ Z

  • Pontos de mínimo

    • f x = - π 2 + 2 k π ,   k ∈ Z

    g x = 3 π 4 + k π ,   k ∈ Z

    h x = - π + 4 k π ,   k ∈ Z

  • Intervalos de crescimento e decrescimento

A f ( x ) tem crescimento em - π 2 + 2 k π , π 2 + 2 k π   k ∈ Z e decrescimento em π 2 + 2 k π , 3 π 2 + 2 k π   k ∈ Z

A g ( x ) tem crescimento em - π 4 + k π , π 4 + k π   k ∈ Z e decrescimento em π 4 + k π , 3 π 4 + k π   k ∈ Z .

A h ( x ) tem crescimento em - π + 4 k π ,   π + 4 k π   k ∈ Z e decrescimento em π + 4 k π , 3 π + 4 k π   k ∈ Z .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g - 5 6 π .
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g - 5 6 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o s t = 0 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e c t = 2 está satisfeita.