Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 31b
Construir o gráfico das seguintes funções trigonométricas. Verificar se são periódicas e em caso afirmativo determinar o período.
- ;
- ;
Passo 1
Para a letra (b) teremos os seguintes gráficos:
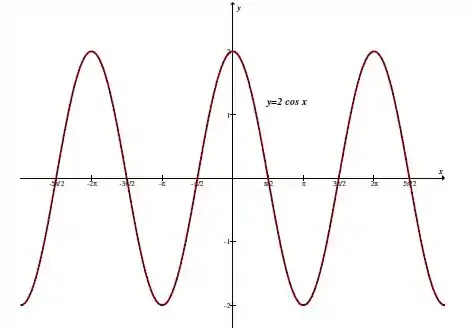
Temos aqui uma função periódica de período igual a .
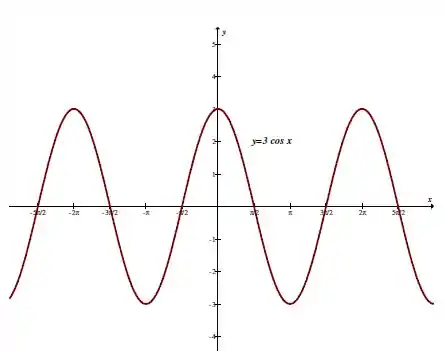
Temos aqui uma função periódica de período igual a .
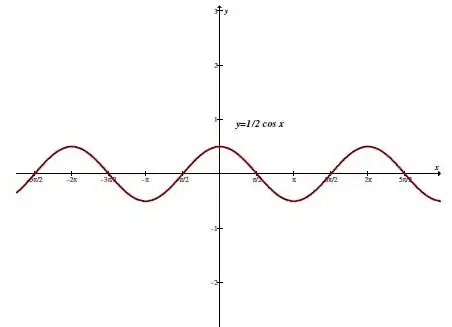
Temos aqui uma função periódica de período igual a .
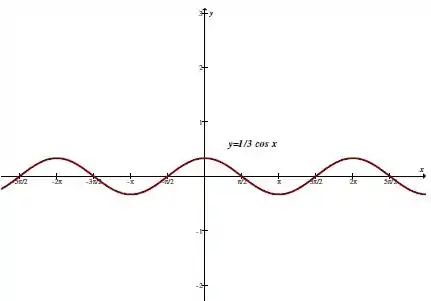
Temos aqui uma função periódica de período igual a .
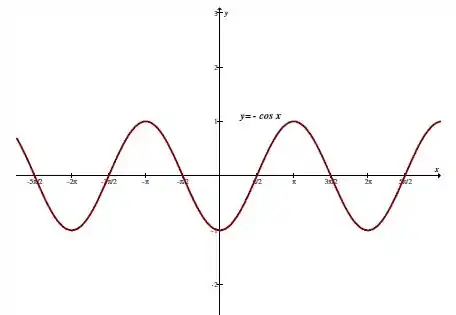
Temos aqui uma função periódica de período igual a .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da