Copie os vetores na figura e use-os para desenhar os seguintes vetores.
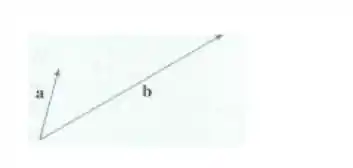
Passo 1
- Para fazer a soma de dois vetores nós devemos unir a pontinha de um com o início do outro e traçar uma reta unindo o início do primeiro com a ponta do segundo.
- Para fazer a diferença entre dois vetores podemos unir os dois pelo seu ponto inicial e traçar uma reta unindo suas pontas e apontando para o primeiro termo da subtração.
- Multiplicar um vetor pelo escalar é a mesma coisa que manter sua direção e sentido, mas dobrar seu tamanho.
- Multiplicar um vetor pelo escalar é a mesma coisa que inverter seu sentido e diminuir pela metade seu tamanho.
- Como já temos o vetor , e já sabemos fazer uma soma de vetores, ficamos com:
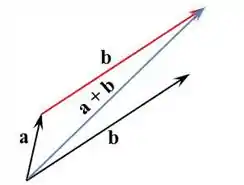
Passo 2
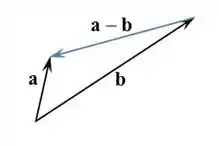
Passo 3
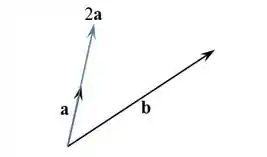
Passo 4
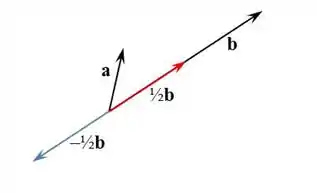
Passo 5
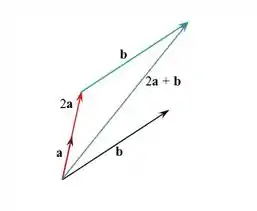
Passo 6
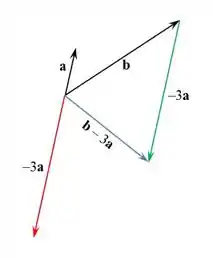
Resposta
Ei, a resposta está no passo a passo :)