Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.8 - Ex. 12
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Oi, pessoal! Tudo bem por aí?
A questão quer que a gente esboce o sólido que é descrito por:
Bom, como temos uma região em função de , o que temos aqui é uma região descrita em coordenadas esféricas.
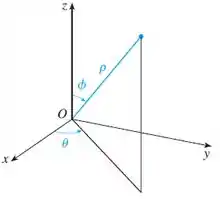
Esquema de representação de um ponto em coordenadas esféricas
Então, vamos analisar variável por variável, achar o comportamento de cada uma e entender qual sólido cada uma dessas variações vão formar.
Vamos lá!
Passo 2
Vamos entender a variação de cada variável no espaço, olhando na imagem do nosso Passo 1.
- : Como essa variável é uma distância radial da origem e nós temos que:
- : Como vemos na imagem do passo , é um ângulo medido a partir do eixo . No nosso caso, temos:
- : Repare como a questão não trouxe restrição nenhuma para então assumimos que ele assume todos os valores possíveis:
Podemos dizer então que no plano nós temos dois círculos, um de raio e outro do raio , ambos com o mesmo centro na origem. Então estamos falando de uma casca esférica com espessura de 1 unidade .
Nosso ângulo parte do plano , onde e vai até a parte negativa do eixo , onde . Isso significa que nosso sólido vai estar totalmente abaixo do plano .
Passo 3
Usando a descrição que achamos, temos nosso sólido. Uma casca esférica, composta por uma esfera dentro da outra (raio interno e raio externo , formando uma espécie de tigela, abaixo do plano .
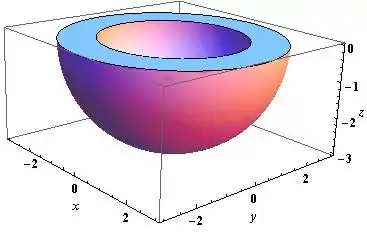
Resposta
.