Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 6
Copie os vetores na figura e use-os para desenhar os seguintes vetores.
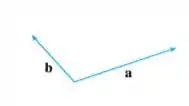
Passo 1
Nesse nós temos que pegar o final do vetor e juntar com o início de .
O vetor que formar ligando as pontas é o vetor soma:
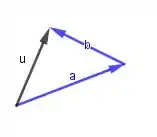
Passo 2
Agora a gente tem que somar com , é o mesmo procedimento do outro, só que antes temos que mudar o sentido do para baixo...
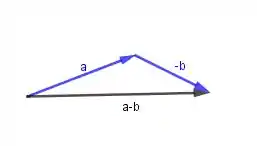
Passo 3
Esse vetor é metade do vetor , só dividir e pegar a metade do comprimento...
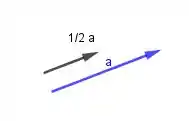
Passo 4
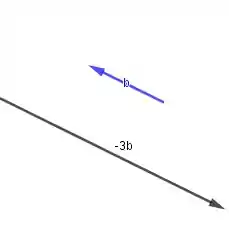
Aqui é o triplo do comprimento do vetor que a gente já usou ali em cima...
Passo 5
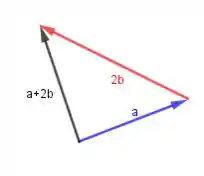
Agora a gente vai somar o vetor com o dobro do vetor , mesmo esquema dos outros...
Passo 6
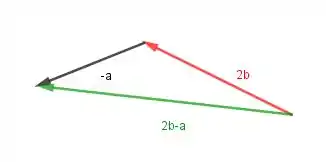
Aqui a gente vai usar o vetor do item anterior, e vamos somar com (aí a gente troca o sentido de ...
Prontinho!!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere as retas ( x , y , z ) = t ( 1,2 , - 3 ) e ( x , y , z ) = ( 0,1 , 2 ) + s ( 2,4 , - 6 ) em R 3 . Encontre a equação geral do plano que contém estas duas retas e ache um subconjunto com o ma
Ache as equações dos planos em R 3 ortogonais ao vetor ( 2,2 , 2 ) , que distam 3 do ponto ( 1,1 , 1 ) . Estes planos são subespaços de R 3 ? Caso afirmativo, encontre base(s) ortonormal (is) para ele
Sejam U e V vetores no espaço, com V ≠ 0 - .a) Determine o número α , tal que U - α V seja ortogonal aV .
Embora não exista o produto vetorial de dois vetores em R n , para n3 , podemos definir o produto vetorial de n - 1 vetores, V 1 = v 11 , … , v 1 n , … v n - 1 = ( v n - 1 1 , … , v n - 1 n como V 1xV
Sejam V 1 , … , V k vetores linearmente dependentes. Mostre que, aplicando-se o processo de ortogonalização de Gram-Schmidt aos vetores V 1 , … , V k , se obtém um vetor W i que é nulo, para algum i =