Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 1
Nos exercícios de 1 a 12, ache os extremos absolutos da função dada no intervalo indicado, se houver algum, e ache os valores de x nos quais os extremos absolutos ocorrem. Faça um esboço do gráfico da função no intervalo.
Passo 1
Seja . Vamos calcular a :
Como , então é sempre crescente. Pelo mesmo motivo, quando , temos que e como não assume valores negativos, 0 é um valor mínimo absoluto.
Passo 2
Para esboçar o gráfico, primeiro vamos encontrar os pontos que a função intercepta os eixos. Primeiro o eixo das ordenadas e, para isso, faremos
Agora, verificando as raízes, já sabemos que é raiz pelo passo 1. Como é crescente sempre, só tem essa raiz.
Passo 3
Calculando para o teste da concavidade, teremos:
Assim como no passo 1, raiz de um número real só pode ser não-negativa, ou seja, sempre. Logo, concavidade para baixo.
Passo 4
Agora que já sabemos o comportamento da função, podemos montar seu gráfico, marcando os pontos notáveis, obedecendo a concavidade e o fato de ser crescente.
Resposta
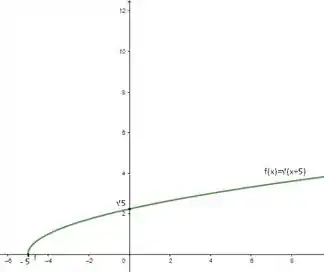
E o ponto mínimo absoluto é .