Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 42
Um copo de papel em forma de cone é feito de maneira a conter de água. Ache a altura e raio do copo que usa a menor quantidade possível de papel.
Passo 1
Eaeee, belezinha?? Bom... a questão quer que calculemos altura e raio do copo que usa a menor quantidade possível de papel.
O dado que a questão nos dá é que o copo tem forma de cone e que é feito de maneira a conter de água.
Para ficar mais fácil a nossa visualização, temos a figura:
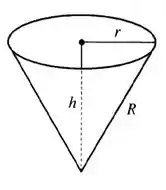
Onde é o raio da base do cone (raio do copo), é a altura e é a hipotenusa do triângulo imaginário formado pelos catetos e .
Então... para calcularmos e , temos que descobrir a função responsável e minimizá-la utilizando derivadas.
Assim, lembre-se que para descobrirmos pontos de máximo ou mínimo, basta derivarmos uma função e igualar a zero!!
E aí? Bora lá aplicar?? 😉
Passo 2
A quantidade de papel diz respeito à superfície da área do cone, que no formato de copo tem a fórmula:
A gente precisa isolar uma das variáveis para conseguir minimizar essa fórmula, aí a gente pode usar esse triângulo retângulo formado na figura por meio de Pitágoras!
Fica assim:
Substituindo em :
Passo 3
Do jeito que a fórmula está torna a nossa resolução chatinha, então vamos usar um passo a mais pra facilitar tudo: usar uma variável pra ficar tranquilo de derivar! Então:
Além dessas fórmulas todas, o exercício dá uma informação muito importante, o volume, e vamos usar ele pra ajudar nas próximas fórmulas:
Substituindo em (juro que esse passo tá acabando!):
ACABOU, MEU CONSAGRADO!!
Passo 4
Minimizando , ou seja, derivando e igualando a zero:
Agora finalmente substituindo em :