Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.2 - Ex. 41
Uma corda é amarrada a um peso e passa por um gancho que está a acima do chão. A corda é puxada passando pelo gancho, a uma velocidade de e arrasta o peso pelo chão. Se o comprimento da corda entre o peso e o gancho for de quando a medida em radianos do ângulo entre a corda e o chão for , ache a variação de em relação ao tempo, em termos de .
Passo 1
Um esquema para ilustrar o problema é mostrado a seguir:
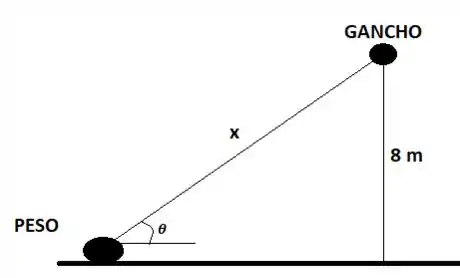
Temos que é o comprimento da corda que liga o peso ao gancho e é o ângulo que a corda faz com o chão. Como a velocidade com que a corda é puxada é , temos que . O sinal negativo vem do fato de diminuir conforme a corda é puxada.
A relação geométrica que devemos escrever é
Passo 2
Derivando essa relação, temos que
Assim,
Como , temos que
Essa é a relação que o enunciado queria que chegássemos: como função de .