Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 28

(a) Se , encontre e .

(b) Verifique que sua resposta para a parte (a) é razoável fazendo os gráficos de , e .

Passo 1

Eaee, belezinha??? Bom... queremos encontrar a primeira e a segunda derivada da seguinte função:

Para isso, precisaremos aplicar a regra do produto, que é dada por:

A gente também precisa ter em mente as seguintes derivadas:

Depois, iremos plotar e suas derivadas a fim de observar se as nossas respostas fazem sentido (por meio do crescimento e decrescimento das derivadas!!).

E aí?? Bora lá?? 😉

Passo 2

Item a:

Para derivarmos a função, devemos utilizar a regra do produto:

Derivando a exponencial e o cosseno, temos:

Colocando a exponencial em evidência:

Passo 3

Para obter , devemos derivar e para isso, usamos novamente a regra do produto:

Derivando a exponencial e distribuindo a derivada (regra da soma/diferença), temos:

Aplicando a derivada do seno e do cosseno:

Colocando a exponencial em evidência:

Passo 4

Item b:

Temos então o gráfico:

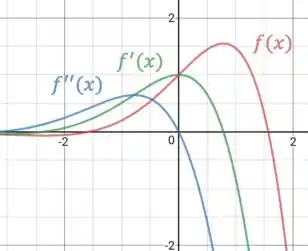
Podemos ver que é razoável pois quando é negativa, está decrescendo, quando é positiva, está crescendo e ao mesmo tempo, quando é negativa, está decrescendo, quando é positiva, está crescendo.