Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.3 - Ex. 27
(a) Se , encontre .
(b) Verifique que sua resposta para a parte (a) é razoável fazendo os gráficos de e para .
Passo 1
Eaee, belezinha?? Bom... queremos calcular a derivada da seguinte função:
Para isso, precisaremos da regra do quociente, pois podemos reescrever essa equação da seguinte forma:
Então para derivarmos o primeiro termo, se faz necessaria a regra do quociente.
Sejam e duas funções deriváveis, então a derivada do quociente é dada por:
Também precisamos saber que:
Onde é um número inteiro.
Agora bora aplicar!! 😉
Passo 2
Item a:
Para derivarmos vamos, primeiramente, reescrever a equação de forma mais simples:
Sabemos que a secante é o inverso do cosseno, logo:
Agora, para derivarmos, podemos aplicar a regra da subtração:
Aplicando a regra do quociente em e da potência em , temos:
Colocando a derivada de :
Simplificando:
Organizando para que possamos aplicar uma identidade trigonométrica:
Reescrevendo:
Passo 3
Item b:
Temos então o gráfico, iremos plotar utilizando o GeoGebra:
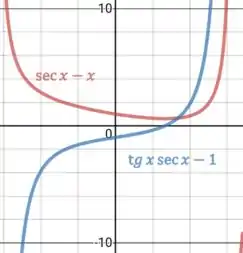
Podemos ver que a função é decrescente enquanto o a derivada é negativa e crescente quando a derivada é positiva.
