Uma cultura de bactérias começa com 500 indivíduos e dobra de tamanho a cada meia hora.

a) Quantas bactérias existem após 3 horas?

b) Quantas bactérias existem após horas?

c) Quantas bactérias existem após minutos?

d) Trace o gráfico da função população e estime o tempo para a população atingir bactérias.

No item a), precisamos encontrar tamanho da população de bactérias depois de 3 horas.

Pra isso, lembramos que a população de bactérias dobra a cada meia hora. Isso significa que, em horas, a população vai ter dobrado 6 vezes. Vamos ver como fica:

Sendo assim, descobrimos que a população depois de horas é de bactérias.

No item b), precisamos encontrar o tamanho da população de bactérias depois de horas. Isso significa que precisamos encontrar uma maneira de expressar o tamanho da população em função do tempo.

Como sabemos que se trata de um crescimento exponencial, vamos partir da sua expressão geral:

A partir das informações que foram dadas, conseguimos determinar os parâmetros e .

Como sabemos que a população inicial é de bactérias, podemos dizer que:

Além disso, sabemos que a população dobra a cada intervalo de tempo. Então concluímos que:

Olha só. A nossa função agora pode ser escrita nessa forma:

Legal! Pra terminar, precisamos lembrar que a população de bactérias dobra a cada meia hora. Então ajustamos dessa forma:

Nossa função fica assim:

No item c), precisamos calcular o tamanho da população depois de minutos. Lembrando que precisa ser expresso em horas, podemos fazer . Dessa maneira, temos:

Vamos tentar simplificar esse expressão trabalhando com as potências:

Utilizando a aproximação , temos:

Para plotarmos o gráfico, vamos calcular o valor da função pra alguns valores.

Vamos ver como esses pontos ficam no gráfico:

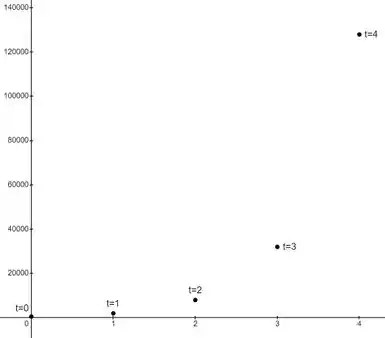
A seguir plotamos um esboço da função e estimamos o encontro com a reta :

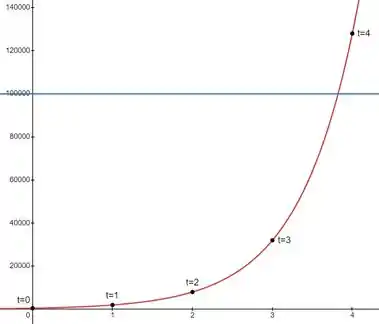
Vemos que a exponencial ultrapassa a reta aproximadamente em . Assim, após aproximadamente 3,8 horas a população de bactérias será superior a .