Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.2 - Ex. 24
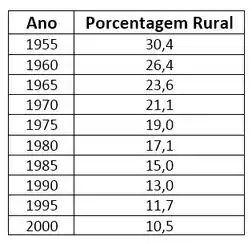
A tabela mostra a porcentagem da população da Argentina que vivia em áreas rurais de 1955 a 2000. Encontre um modelo para os dados e use-o para estimar a porcentagem de população rural em 1988 e 2002.
Passo 1
Fala galera!
A tabela mostra a porcentagem da população argentina que vivia em áreas rurais em diferentes anos.
Queremos encontrar um modelo que descreva esse comportamento. Em outras palavras, queremos uma função que represente esse fenômeno.
Pra isso, vamos plotar os dados da tabela, depois escolher um tipo de função adequada e encontrar os coeficientes necessários.
Com esse resoltado, vamos estivar os valores da função pra 1988 e 2002.
Passo 2
Com os dados da tabela, vamos plotar os pontos num gráfico e obter um diagrama de dispersão:
Com isso a gente entende mais ou menos como esse fenômeno ocorre. E aparentemente um modelo exponencial decrescente deve descrever esses dados.
Então vamos tentar um ajuste do tipo
Coloquei para definir como o valor de onde que é nossa origem de tempo!
Passo 3
Fazendo o ajuste no excel, vemos a curva que mais se aproxima desses dados. Você pode ver que é diferente de ligar os pontos, a curva não passa exatamente em alguns deles, mas é um modelo muito próximo, que representa o fenômeno como um todo.
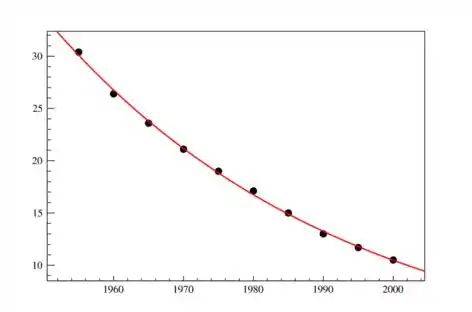
Do software, os valores encontrados para os parâmetros do ajuste são:
Portanto,
Passo 4
Mas uma outra forma de resolver é pegar 2 pontos exatamente em cima da curva e montar um sistema. São 2 pontos porque temos 2 coeficientes pra encontrar.
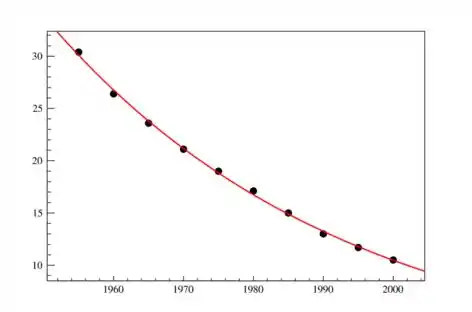
E aqui a gente tem que perceber aquilo que eu falei acima, que o modelo não vai passar exatamente em todos os pontos, então vamos escolher os mais certinhos:
Substituindo em , temos o sistema:
Resolvendo, a gente deve encontrar valores muito próximos dos dados pelo software.
Passo 5
Agora que temos o modelo, precisamos estimar a porcentagem de população rural em 1988 e 2002.
Para :
Já para :