Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 35
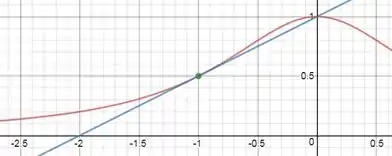
a) A curva é chamada de bruxa de Maria Agnesi. Encontre a equação para a reta tangente a essa curva no ponto .
b) Ilustre a a parte (a) fazendo o gráfico da curva e da reta tangente na mesma tela.
Passo 1
E aí! tudo certinho?
Precisamos achar a equação da reta tangente à curva no ponto dado.
Para isso, precisamos derivar a função para achar o coeficiente angular da reta tangente e assim usar a equação da reta, que é dada por:
Em que é o coeficiente angular da reta, que encontraremos derivando.
Veja só! 😊
Passo 2
Vamos achar o coeficiente angular da reta tangente derivando a função pela regra do quociente.
A regra do quociente é dada por:
Aplicando:
Substituindo para encontrarmos o valor do coeficiente angular no ponto requerido:
Tranquilo até aqui? 👀
Passo 3
Usando , e na equação da reta:
Bacana, não é? 😉
Passo 4
Em vermelho temos a curva e em azul a reta tangente. Nosso gráfico foi gerado com o auxilio do GeoGebra.
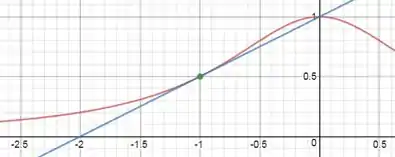
E aí! o que achou? Responde Aí! 😁
Resposta
a) .
b) 