Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.1 - Ex. 58
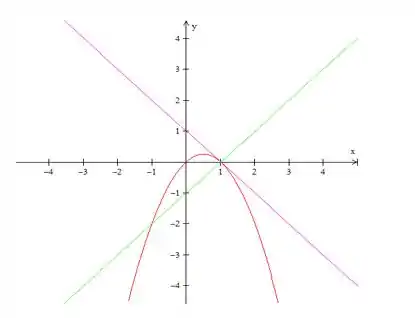
Onde a reta normal à parábola no ponto intercepta a parábola uma segunda vez? Ilustre com um esboço
Passo 1
Fala aí, galerinha! 😉
Queremos saber em que ponto a reta normal à parábola dada por , normal no ponto , a corta pela segunda vez.
Tem ideia de como fazemos isso? 😉
Vamos achar primeiro o coeficiente angular da reta tangente que passa por .
Depois encontramos o coeficiente da reta normal sabendo que
E por ultimo obtermos a equação da reta normal
Veja só! 😁
Passo 2
Seja o coeficiente da reta tangente a parábola no ponto .
Então, . A derivada de é e, com isso, descobrimos o valor de :
Sabe-se que o coeficiente angular da reta normal é dado por:
Logo, a equação da reta normal será:
Basta, agora, fazer a interseção da parábola com essa reta normal para acharmos os pontos de interseção, assim:
Para
Obtemos o ponto que já foi dado.
O segundo ponto que queremos achar é para
e assim, obtemos o segundo ponto de interseção
Tranquilo até aqui? 😎
Passo 3
Esboçando o gráfico de , e
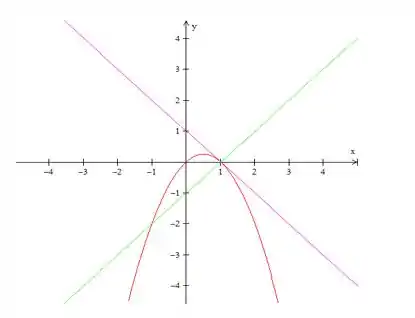
E aí! o que achou? Responde Aí! 😉
Resposta
