Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.4 - Ex. 56
-
A curva É chamada curva ponta de bala. Encontre uma equação da reta tangente a essa curva no ponto .
- Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Passo 1
Fala aí, tudo bem com você?
Bom, essa questão deu pra gente a curva:
E pediu pra gente encontra a equação da reta tangente a essa curva no ponto .
Além disso, precisaremos fazer o gráfico desta curva e da sua curva tangente na mesma tela.
E para encontrar a equação da reta tangente, faremos:
O valor é a inclinação da reta, e é achado calculando a primeira derivada da função e aplicando o valor do ponto pedido.
Show, vamos fazer isso juntos.
Passo 2
a) Nossa curva é dada por:
Para , nós temos que , assim ficamos com a expressão:
Primeiro vamos arrumar um pouco essa função:
Maravilha.
Passo 3
E para encontrar o coeficiente angular da nossa reta tangente, precisamos fazer a derivada de . Como ele é formado por uma multiplicação entre duas outras funções, podemos usar a regra do produto:
Temos que:
Vamos calcular , usando a regra do polinômio:
e
Vamos agora derivar , usando a regra da cadeia, da função constante e do polinômio:
e
Assim,
Passo 4
Agora é só substituir na expressão:
Passo 5
Vamos agora aplicar no ponto :
Ou seja, nosso coeficiente angular da reta tangente é:
Passo 6
Agora é só substituir na fórmula da equação da reta, utilizando o ponto dado:
Substituindo tudo que encontramos até aqui, ficamos com:
E nossa reta tangente será:
Passo 7
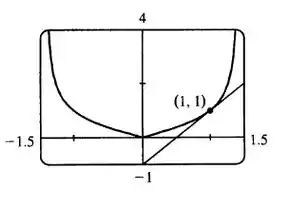
b) Ilustração do gráfico:
Veja que nossa reta tangencia o gráfico da função no ponto e tem uma inclinação crescente como vimos na resolução.
E assim, concluímos mais uma questão.
Resposta
a)
b)
