Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 84

Trace um diagrama ilustrando duas retas perpendiculares que se interceptam sobre o eixo y , ambas tangentes à parábola y = x 2 . Onde essas retas se interceptam.

Passo 1

Nessa questão, nos é pedido para traçar uma diagrama ilustrando duas retas perpendiculares que se interceptam sobre o eixo y e que ambas são tangentes à parábola y = x 2 .

Queremos saber em que ponto do eixo y as retas se interceptam.

Os pontos verdes são os pontos de tangência e o ponto azul, o ponto de interseção. A parábola y = x 2 está em vermelho e as retas são perpendiculares.

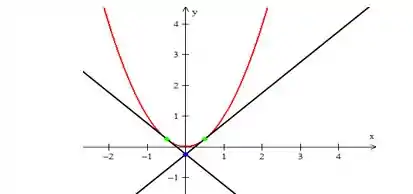
Pelo gráfico, podemos perceber a simetria da parábola. Desta forma, devido à simetria, um ponto de tangência é o ponto ( x 0 , y 0 ) e o outro ( - x 0 , y 0 ) .

Como se interceptam sobre o eixo y , então o ponto de interseção é o ponto ( 0 ,   c ) sendo c < 0 .

Como essas retas são tangentes à função y = x 2 , podemos encontra-las fazendo a equação da reta tangente que é:

y - y 0 = m x - x 0

E m é a inclinação da reta que pode ser calculado fazendo a derivada da função no ponto dado.

Além disso, as retas são perpendiculares, portanto a inclinação de uma tem relação com a inclinação da outra, dada por:

m 1 = - 1 m 2

Passo 2

Vamos, então, primeiro achar as equações das duas retas.

A derivada de y da parábola é y ' = 2 x .

Sabe-se que a inclinação da reta tangente em x 0 , y 0 é m 1 = y ' x 0 , y 0 = 2 x 0

E no ponto ( - x 0 , y 0 ) é m 2 = y ' - x 0 , y 0 = - 2 x 0

Como as retas são perpendiculares, então tem-se que   m 1 = - 1   m 2

Assim temos:

2 x 0 = - 1 - 2 x 0  

4 x 0 2 = 1

x 0 2 = 1 4

x 0 = ± 1 2

Consideramos na nossa análise que x 0 era positivo.

Ou seja, um ponto de tangência é x 0 = 1 2 e o outro ponto de tangência é - x 0 = - 1 2 .

E podemos encontrar as inclinações das retas tangentes.

Logo,

m 1 = 2 x 0 = 2 1 2 = 1

e

m 2 = - 2 x 0 = - 2 1 2 = - 1

Passo 3

Agora, vamos voltar para a equação da reta tangente. Primeiro a reta de inclinação m 1 , temos:

y - y 0 = m x - x 0

Sabemos que essa reta é tangente à função f x = x 2 quando x 0 = 1 / 2 , dessa forma podemos encontrar a coordenada x 0 , y 0 , substituindo 1 / 2 na equação da função f x .

y 0 = 1 2 2 = 1 4

Dessa forma, temos a seguinte equação:

y - 1 4 = 1 x - 1 2

y = 1 4 + x - 1 2

y = x - 1 4

Agora basta ver onde essa reta intercepta o eixo y , ou seja, fazer x = 0 .

y = - 1 4

Isso já basta... mas se você quiser fazer a prova real, vamos olhar para a segunda reta.

y - y 0 = m 2 x - x 0

Para essa reta, o ponto que ela tangencia a curva é - x 0 = - 1 2

E o ponto y 0 pode ser encontrado substituindo – x 0 = - 1 2 na função x 2

y 0 = - 1 2 2 = 1 4

Dessa forma, temos:

y - 1 4 = - 1 x + 1 2

y = - x - 1 2 + 1 4

y = - x - 1 4

E fazendo x = 0 , também obtemos:

y = - 1 4

Ou seja, as retas passam pelo ponto 0 , - 1 4 aonde se interceptam sobre o eixo y .

Resposta

As retas se interceptam no ponto ( 0 , -   1 4   )   .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine beta para que y = beta x - 2 seja tangente ao gráfico de f (x) = x^3 - 4 x .
Sabe-se que r é uma reta que passa pela origem e que é tangente ao gráfico de f x = x 3 + 2 x 2 - 3 x . Determine r .
A reta s para pelo ponto 3,0 e é normal ao gráfico de f x = x 2 no ponto a , b .a) Determine a , b .b) Determine a equação de s .
Determine a equação de uma reta, não vertical, que passa pelo ponto 0 , 4 3 e que seja normal ao gráfico de y = x 3 .
Sejam A e B os pontos em que o o gráfico de f x = x 2 - α x , α real, intercepta o eixo x . Determine α para que as retas tangentes ao gráfico de f em A e em B , sejam perpendiculares.