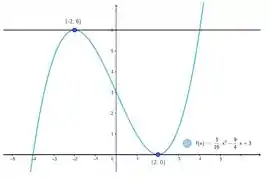
Encontre uma função cúbica cujo gráfico tenha tangentes horizontais nos pontos e .

Tá, mas o enunciado quer tangente horizontal, certo? Sim, é por isso que a gente precisa achar os parâmetros de forma que o coeficiente angular seja nulo, ou seja:

Além disso, vamos lembrar que os pontos de tangência fazem parte da curva! Portanto é igualmete importante considerar que:

O enunciado diz pra gente quem é e também! Que são os pontos de tangência e .

Na prática então vamos procurar valores de que satisfaçam:

Vamos lá!

Vamos começar vendo as duas primeiras condições, que falam da primeira derivada da função. Seja:

Teremos como derivada:

Substituindo o ponto de tangência , temos:

Como sabemos que ou , ganhamos duas equações:

Mas as retas precisam ser horizontais, então essas derivadas precisam ser zero. Assim, temos:

E

Galera, olha a malandragem. Já que obtivemos equações, deu pra ver que a ideia é montar um sistema. Mas como são variáveis, , vamos precisar de equações! As outras duas vão vir de:

Seja:

Temos no ponto de tangência:

E como e , ganhamos as nossas últimas duas equações:

E

O que é o mesmo que:

E

Tranquilo até aqui? 😉

Temos que resolver então o sistema com as quatro equações:

Se somarmos a equação com a , achamos:

Se fizemos equação menos a equação , achamos:

Usando dentro de , concluímos que:

Usando e dentro de e , fazemos um novo sistema:

Fazendo duas vezes mais obtemos:

Jogando dentro de achamos:

Juntando , fechamos a equação de

Uffa!!

E só pra ajudar a gente, saca só a comprovação gráfica:

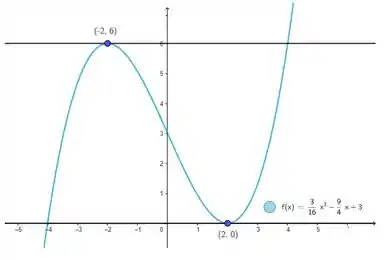
Valeu, galera! Até a próxima! 😉