Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.5 - Ex. 34
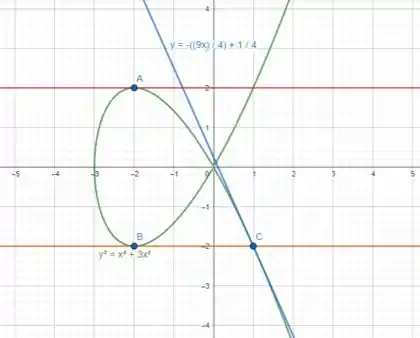
A curva com equação é denominada cúbica de Tschirnhausen. Encontre uma equação da reta tangente a essa curva no ponto .
Em que pontos essa curva tem uma tangente horizontal?
Ilustre as partes e fazendo o gráfico da curva e das retas tangentes sobre uma tela comum.
Passo 1
Eaee, belezinha?? Bom... O enunciado pede a equação da reta tangente à uma curva dada por:
No ponto .
Para acharmos da equação de uma reta, precisamos de duas informações: um ponto em que ela passa (o enunciado já forneceu) e sua inclinação.
Assim, podemos usar a equação da reta na forma ponto-inclinação:
Onde representa a inclinação (ou coeficiente angular da reta) e , os pontos dados.
Para a reta tangente, será a derivada de com relação a , isto é, no ponto de tangência.
Assim, para encontrar , devemos derivar implicitamente a equação fornecida.
Também queremos encontrar pontos essa curva tem uma tangente horizontal.
Para isso, a inclinação deve ser igual a zero, ou seja, deveremos igualar a derivada a zero para encontrar os pontos!!
Por fim, também queremos plotar o gráfico da curva e da reta tangente.
Agora bora lá!! 😉
Passo 2
Bom galera, para encontrar a equação da reta tangente a curva devemos derivar a equação da curva em relação a .
A curva apresentada é .
Utilizaremos a derivação implícita para encontrar :
Veja que ao diferenciar , multiplicamos pela sua derivada . Isso ocorre devido a regra da cadeia.
Vamos agora isolar :
O enunciado nos dá o ponto .
Vamos substituir o ponto dado em :
Nosso é o coeficiente angular da nossa reta tangente.
Passo 3
Podemos encontrar a equação da reta tangente utilizando a fórmula
Lembre-se que .
Onde e são as coordenadas do ponto dado. Substituindo na formula, temos
Nossa equação da reta tangente a curva é
Passo 4
Nossa curva possui uma tangente horizontal quando .
Substituindo na expressão encontrada no item , temos:
Colocando em evidência, temos
Dessa forma, ou . Se , então e assim, não existe. Portanto, nesse caso .
Substituindo , temos:
pode ser ou .
Assim, nossa curva possui uma tangente horizontal nos pontos e .
Passo 5
Ilustrando graficamente os itens e , temos a seguinte imagem:
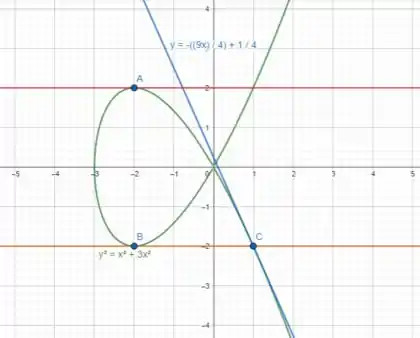
Podemos ver as tangentes horizontais em e , ou seja, nos pontos A e B, respectivamente.
Podemos também ver a reta tangente a curva no ponto , ou seja, no ponto C.
Entendeu direitinho?? Responde aee 😉
Resposta
e
