Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 66

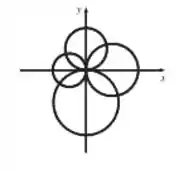
Duas curvas são ortogonais se suas retas tangentes forem perpendiculares em cada ponto de interseção. Mostre que as famílias dadas de curvas são trajetórias ortogonais uma em relação à outra, ou seja, toda curva de uma família é ortogonal a toda curva da outra família. Esboce ambas as famílias de curvas no mesmo sistema de coordenadas.

x 2 + y 2 = a x

x 2 + y 2 = b y

Passo 1

E aí, pessoal! 😊

Bom, galera, nesse exercício queremos mostrar que as curvas apresentadas são ortogonais, ou seja, perpendiculares, e esboçar graficamente essas curvas.

Para isso, iremos utilizar a derivação implícita e comparar o coeficiente angular das curvas e suas retas tangentes. Caso o coeficiente angular de uma reta tangente à curva for a recíproca negativa do coeficiente da outra curva, as trajetórias são ortogonais uma em relação a outra.

Ambas as equações são equações da circunferência, só que uma é deslocada no eixo   x e outra no eixo y . Vamos esboçar o gráfico no final.

Veja só! 😉

Passo 2

Vamos utilizar a derivação implícita para encontrar a inclinação da reta tangente a curva

x 2 + y 2 = a x

2 x + 2 y y ' = a

Agora, vamos isolar y ' , que é a inclinação da reta tangente a curva que derivamos

2 y y ' = a - 2 x

y ' = a - 2 x 2 y

Em um ponto arbitrário P =   ( x 0 ,     y 0 ) , a inclinação da reta tangente é

y ' = a - 2 x 0 2 y 0

Tranquilo até aqui? 😁

Passo 3

Vamos fazer o mesmo para a outra curva para encontrar y '

x 2 + y 2 = b y

2 x + 2 y y ' = b y '

Agora, vamos isolar y ' , que é a inclinação da reta tangente a curva que derivamos

2 y y ' - b y ' = - 2 x

y ' = - 2 x 2 y - b

Em um ponto arbitrário P =   ( x 0 ,     y 0 ) , a inclinação da reta tangente é

y ' = - 2 x 0 2 y 0 - b

Repara que os coeficientes angulares encontrados ( y ' ) de cada curva é a reciproca negativa do outro, ou seja, elas são ortogonais. A gente consegue ver isso, pois o que ta no denominador de uma é o numerador do outro.

E aí! O que achou? Responde Aí! 😊

Resposta

Assim, se as curvas se interceptam em P =   ( x 0 ,     y 0 ) e a e b são diferentes de 0 , então as curvas são ortogonais. Graficamente

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + x y + y 2 = 3 , ( 1,1 ) (elipse)
A curva com equação 2 y 3 + y 2 - y 5 = x 4 - 2 x 3 + x 2 tem sido comparada com um “vagão sacolejante”. Use um SCA para fazer essa curva e descubra o porquê desse nome.Em quantos pontos essa curva te
Formas extravagantes podem ser criadas usando-se a capacidade de traçar funções definidas implicitamente de um SCA.Faça o gráfico da curva com equação y y 2 - 1 y - 2 = x x - 1 x - 2 Em quantos pontos
Use derivação implícita para encontrar a equação da reta tangente da curva no pontos dados. x 2 - x y - y 2 = 1 , 2,1 (hipérbole)
28. Use a derivação implícita para encontrar a equação da reta tangente à curva no ponto dado. x 2 + 2 x y - 4 y ² = 12 ² , ( 2,1 ) (elipse)