Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.Exercícios adicionais e avançados - Ex. 34

Tempo entre doses de medicamentos (Continuação do Exercício 33.) Se um medicamento é conhecido por ser ineficaz abaixo de uma concentração C L e perigoso acima de certa concentração mais alta C H , é preciso encontrar valores de C 0 e t 0 que produzirão uma concentração que seja segura (não acima de C H ) mas eficaz (não abaixo de C L ). Veja a figura a seguir. Portanto, queremos encontrar os valores para C 0 e t 0 para os quais

R = C L     e   C 0 + R = C H

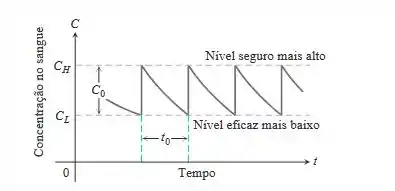
Assim, C 0 = C H - C L . Quando esses valores são substituídos na equação para R obtida no item (a) do Exercício 33, a equação resultante fica simplificada para

t 0 = 1 k ln ⁡ C H C L

Para encontrar um nível eficaz rapidamente, pode-se ministrar uma dose alta que iria produzir uma concentração de C H   m g / m L . Isso poderia ser seguido a cada t 0 horas por uma dose que eleve a concentração por C 0 = C H - C L   m g / m L .

a. Verifique a equação anterior para t 0 .

b. Se k = 0,05   h - 1 e a concentração segura é e vezes a concentração eficaz mais baixa, encontre o período de tempo entre as doses que irá assegurar concentrações seguras e eficazes.

c. Dados C H = 2   m g / m L , C L = 0,5   m g / m L e k = 0,02   h - 1 , determine um esquema para a administração do medicamento.

d. Suponha que k = 0,2   h - 1 e que a mais baixa concentração eficaz seja 0,03   m g / m L . Uma dose única que produz uma concentração de 0,1   m g / m L é administrada. Por quanto tempo o medicamento permanecerá eficaz?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

A - Dado que R = C L e C 0 + R = C H . A equação para R obtida na letra (a) do exercício 33 é igual a

R = C 0 e k t 0 - 1

Podemos escrever essa igualdade da seguinte forma

R e k t 0 - R = C 0 → R e k t 0 = R + C 0

Como R + C 0 = C H , podemos fazer a substituição direta

R e k t 0 = C H → e k t 0 = C H R

Nesse caso, temos que C L = R

e k t 0 = C H C L

Aplicando l n nos dois lados

k t 0 = ln ⁡ C H C L → t 0 = 1 k ln ⁡ C H C L

Passo 2

B – Se k = 0,05   h - 1 e C H C L = e . Então o período entre as doses que garantirá concentrações seguras e eficazes é

t 0 = 1 k ln ⁡ C H C L

Fazendo a substituição, obtemos

t 0 = 1 0,05 ln ⁡ e = 20   h o r a s

C – Dado que C H = 2 m g m L ,   C L = 0,5   m g / m L e k = 0,02   h - 1 . Portanto,

t 0 = 1 0,02 ln ⁡ 2 0,5 ≈ 69,31   h o r a s

D - Dado que C H = 0,1 m g m L ,   C L = 0 , 03   m g / m L e k = 0,2   h - 1 . Portanto

t 0 = 1 0,2 ln ⁡ 0,01 0,03 ≈ 6   h o r a s

Resposta

a )   t 0 = 1 k ln ⁡ C H C L

b )   t 0 ≈ 20   h o r a s

c )   t 0 ≈ 69,31   h o r a s

d )   t 0 ≈ 6   h o r a s

Exercícios de Livros Relacionados

O significado da representação decimal de um número 0 , d 1 d 2 d 3 … (onde o algarismo d i é um dos números 0 ,1 ,2 , … ,9 ) é que 0 , d 1 d 2 d 3 … = d 1 10 + d 2 10 2 + d 3 10 3 + d 4 10 4 + … Most
Use a soma dos dez primeiros termos para aproximar a soma da série. Estime o erro. ∑ n = 1 ∞ n n + 1 3 n
Use a soma dos dez primeiros termos para aproximar a soma da série. Estime o erro. ∑ n = 1 ∞ 1 1 + 2 n
O conjunto de Cantor, cujo nome é uma homenagem ao matemático alemão Georg Cantor (1845-1918), é construído como a seguir. Começamos com o intervalo fechado 0 ,1 e removemos o intervalo aberto 1 3 , 2
Encontre a série de Maclaurin de f e seu raio de convergência. Você pode usar o método direto (a definição de série de Maclaurin) ou séries conhecidas, como a série geométrica, a série binomial ou a s