Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.2 - Ex. 45
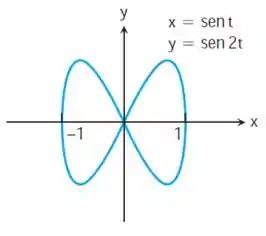
As curvas nos Exercícios 45 e 46 são denominadas curvas de Bowditch ou figuras de Lissajous. Em cada um dos casos, encontre o ponto no interior do primeiro quadrante em que a tangente à curva é horizontal, e encontre as equações das duas tangentes na origem.
Passo 1
Oi galerinha, vem comigo!
Quando varia, o ponto varia e traça a curva , que é chamada de curva parametrizada. Essa curva parametrizada é derivável em se e forem deriváveis em . Então as derivadas , e estão relacionadas pela Regra da Cadeia:
Se as três derivadas existem e , a tangente da curva em é dada pela seguinte equação:
Do enunciado temos os seguintes dados:
Então, primeiramente iremos calcular as derivadas de e :
Sendo assim o coeficiente angular da reta é:
Passo 2
Queremos encontrar o ponto no interior do primeiro quadrante em que a tangente à curva é horizontal. Então, vamos definir o intervalo do primeiro quadrante que é:
Como queremos a reta horizontal, então , assumindo valores de no intervalo restrito, encontramos:
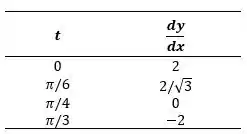
Podemos observar que o ponto que estamos procurando é quando , logo:
O ponto no interior do primeiro quadrante onde a tangente é uma curva horizontal é .
Passo 3
Por fim, precisamos calcular as equações das duas tangentes na origem. Como já sabemos, a tangente é uma reta, logo, a equação da reta é:
Onde:
- coeficiente angular;
- coeficiente linear.
- :
- :
- .
Como o ponto é na origem, sabemos que . E na origem sabemos também que e , com esses dados conseguimos encontrar o valor de , para:
Então a equação é:
Então a equação é:
Tchau pessoal.
Resposta
Resposta
Ei, a resposta está no passo a passo :)