Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.2 - Ex. 40

A maioria dos cálculos de centroide para curvas é feita com uma calculadora ou computador que possua um programa de avaliação de integrais. Como aplicação disso, encontre, com precisão centesimal, as coordenadas do centroide da curva

Passo 1

Olá pessoal, esse exercício é um pouco complicadinho, mas vem comigo que vou te ajudar no passo a passo.

Se uma curva C é definida parametricamente por x = f t e y = g t , a ≤ t ≤ b , em que f ' e g ' são contínuas e não simultaneamente zero em a ,   b , e C é percorrida exatamente uma vez quando t aumenta de a até b , então o comprimento de C é:

L = ∫ a b d x d t 2 + d y d t 2 d t

Então com os valores do enunciado:

Vamos primeiramente calcular as derivadas:

d x d t = 3 t 2

d y d t = 6 t 2 = 3 t

Então conseguimos calcular d m :

d m = d x d t 2 + d y d t 2 d t

d m = 3 t 2 2 + 3 t 2 d t = 9 t 4 + 9 t 2 d t = 9 t 2 t 2 + 1 d t

d m = 3 t t 2 + 1   d t

Passo 2

Para encontrarmos as coordenadas do centroide, precisamos das equações:

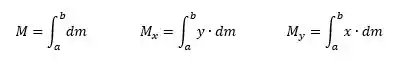
Então, vamos calcular a massa da curva:

M = ∫ 0 3 3 t t 2 + 1 d t = 3 ∙ ∫ 0 3 t 2 + 1 ∙ t d t

Para resolvermos essa integral, iremos considerar:

u = t 2 + 1

Logo:

d u = 2 t d t → t d t = d u 2

Então nossa integral fica da seguinte forma:

= 3 ∙ ∫ u d u 2 = 3 2 ∙ ∫ u d u = 3 2 ∙ ∫ u 1 2 d u = 3 2 ∙ 2 3 ∙ u 3 / 2 = u 3 / 2

Voltando para a integral original:

M = t 2 + 1 3 / 2 0 3 = 4 3 / 2 - 1 3 / 2

M = 7

Passo 3

O momento da curva em relação ao eixo x :

M x = ∫ 0 3 3 t 2 2 ∙ 3 t ∙ t 2 + 1 d t = ∫ 0 3 9 t 3 2 ∙ t 2 + 1 d t

= 9 2 ∙ ∫ 0 3 t 3 ∙ t 2 + 1 d t

Para esta integral, precisamos dividir ela em algumas partes para conseguirmos resolver, mas calma que iremos por passo. Vamos considerar:

u = t 2

Logo:

d u = 2 t d t → t d t = d u 2

Então temos:

= 9 2 ∙ ∫ u ∙ u + 1 d u 2 = 9 4 ∙ ∫ u ∙ u + 1 d u

Porém agora, vamos considerar:

s = u + 1

d s = d u

= 9 4 ∙ ∫ s - 1 ∙ s d s

E por fim, desta integral, vamos considerar:

v = s → s = v 2

Logo:

d v = 1 2 s d s → d s = 2 v d v

= 9 4 ∙ ∫ v v 2 - 1 2 v d v = 9 2 ∙ ∫ v 4 - v 2 d v

Agora conseguimos resolver esta integral:

= 9 2 ∙ v 5 5 - v 3 3

Substituindo os valores, temos:

M x = 9 2 ∙ t 2 + 1 5 5 - t 2 + 1 3 3 0 3 = 9 2 ∙ 2 5 5 - 2 3 3 - 1 5 - 1 3

M x = 87 5

Passo 4

O momento da curva em relação ao eixo y :

M y = ∫ 0 3 t 3 ∙ 3 t ∙ t 2 + 1 d t = 3 ∙ ∫ 0 3 t 4 ∙ t 2 + 1 d t

Utilizando o programa computacional WolframAlpha para resolvermos essa integral, obtemos:

M y = 16,48491

Passo 5

Por fim, conseguimos calcular as coordenadas do centroide:

x - = M y M = 16,48491 7

x - = 2,355

y - = M x M = 87 5 7 = 87 5 ∙ 1 7

y - = 87 35

Espero que eu tenha conseguido te ajudar. Até mais pessoal.

Resposta

x - = 2,355 .

y - = 2,486 .

Exercícios de Livros Relacionados

O que é uma parametrização de uma curva no plano x y ? Uma função y=f ( x ) sempre tem uma parametrização? São parametrizações de uma curva única? Dê exemplos.
O que é uma cicloide? Quais são as equações paramétricas típicas para cicloides? Quais propriedades físicas contam para a importância das cicloides?
Dê algumas parametrizações típicas para retas, círculos, parábolas, elipses e hipérboles. Quanto uma curva parametrizada poderia ser diferente do gráfico de sua equação cartesiana?
Como você pode algumas vezes encontrar a área delimitada por uma curva parametrizada e um dos eixos coordenados?
Qual é a fórmula para o coeficiente angular d y d x de uma curva parametrizada x=f ( t ) ,y=g ( t ) ? Quando a fórmula é aplicada? Quando você pode esperar conseguir encontrar d 2 y d x 2 também? Dê e