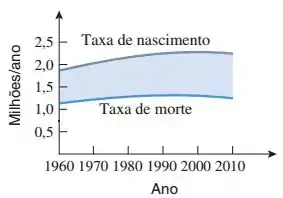
As curvas da figura abaixo modelam as taxas de nascimento e morte (em milhões de pessoas por ano) de um certo país durante um período de anos. O que representa a área entre as curvas acima do intervalo ? Justifique sua resposta.

Vamos pensar aqui. Podemos escrever a taxa de nascimento como:

Com em anos. E a taxa de morte como:

Porque elas são taxas de variação de uma grandeza ao longo do tempo, ou seja, derivadas.

A gente pode escrever essa área assim:

Mas a gente sabe que quando integramos uma derivada, voltamos a função inicial:

Repara que é o aumento da população em um ano. Quando a gente diminui esse valor entre dois anos, estamos verificando o aumento da população de um ano para outro. Logo a área é igual ao crescimento da população em em relação a .