Encontrar a área da região limitada pelas curvas dadas.
Passo 1
A região é essa:
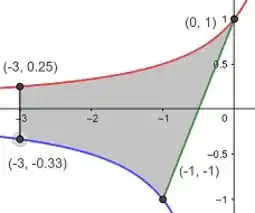
Passo 2
Aqui a gente vai ter que dividir a região em duas.
A primeira região a gente vai considerar as funções de vermelho e azul, que são respectivamente, e . E aí o intervalo vai ser de . Vai ser assim:
(o é negativo nos dois intervalos, então a função do módulo é negativa)
Deixa assim por enquanto...
Passo 3
Agora vamos pra segunda região, que vai de . Nesse intervalo, as funções que estão presentes são .
Aí a área vai ser:
Passo 4
Agora a gente soma as duas áreas:
Prontinho! Essa é a área da região pedida😊