Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.4 - Ex. 36
Calcular a área da parte da circunferência
Que está acima da reta .
Passo 1
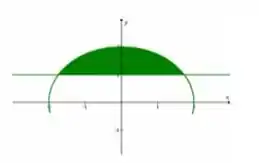
Vamos encontrar os limites de integração cartesianos. Primeiro vamos substituir nas equações:
Agora vamos achar a que valor de corresponde o ponto , limite superior da nossa área:
Repare que, como nossa figura é simétrica, poderíamos integrar em de ou integrar em de e multiplicar o resultado por dois, que é o que vamos fazer.
Integrando:
Aplicando os limites:
Resposta
Exercícios de Livros Relacionados
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Em cada exercício, suponha que f e g sejam funções contínuas distintas de [ a , b ] e que A denote a área da região delimit
Dê uma estimativa para a área da região do primeiro quadrante englobada por y = s e n2 x e y = a r c s e nx .
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. y = 1 x 1 - ln x 2 , y = 3 x
Use um recurso gráfico computacional, quando necessário, para encontrar a área da região englobada pelas curvas. x = y 3 - 4 y 2 + 3 y , x = y 2 - y