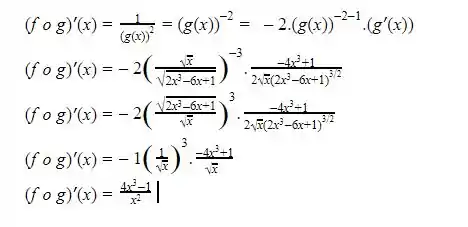Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.7 - Ex. 50
50. Dada e , ache a derivada de de duas maneiras: (a) encontrando primeiro usando a regra da cadeia
Letra (a)
Passo 1
Nesta opção estamos trabalhando com o conceito de função composta. Em que para encontrar f o g basta no lugar do u da f(u) aplicar a g(x).
Passo 2
Sendo assim, f o g é igual a
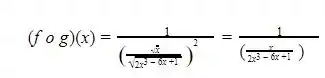
Passo 3
A derivada de f o g é dada por
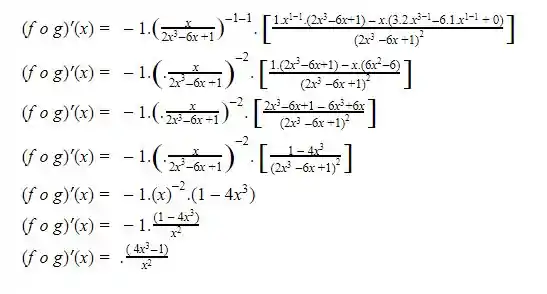
Letra (b)
Passo 4
Utilizando a regra da cadeia teremos
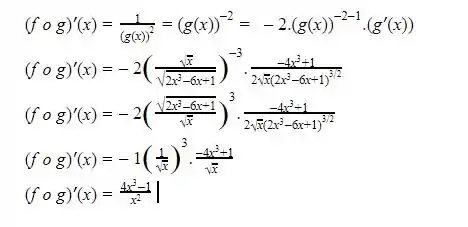
Resposta
Exercícios de Livros Relacionados
Suponha que as funções g t e h t sejam definidas para qualquer valor de t , tal que g 0 = h 0 = 0 . Pode lim t→0 g t h t existir? Se sim, deve ser igual a zero? Justifique sua resposta.
Alguma tangente à curva y = x cruza o eixo x em x=- 1 ? Se sim, determine uma equação para a reta e o ponto de tangência. Se não, por que não?
A parábola y = 2 x 2 - 13 x + 5 tem alguma tangente cujo coeficiente angular seja - 1 ? Se assim for, determine uma equação para a reta e para o ponto de tangência. Se não tem, por que não?
Determine a derivada f ' x da função dada y=f( x) . Faça os gráficos de y=f ( x ) e y= f ' ( x ) lado a lado empregando planos coordenados diferentes e responda às questões a seguir. Para que valores
Determine a derivada f ' x da função dada y=f( x) . Faça os gráficos de y=f ( x ) e y= f ' ( x ) lado a lado empregando planos coordenados diferentes e responda às questões a seguir. Para que valores