Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 29a
29. Dada
- Determine um valor de b para o qual é contínua em b.
- é derivável em b encontrado na parte (a) ?
Letra (a)
Passo 1
Para determinar se f(x) é continua em um ponto deve-se atender a 3 pré-requisitos, ou seja , para uma função ser continua em x0:
f(x0) tem que existir;
tem que existir;
.
Assim, deve-se verificar cada um dos itens ácima para dizer se f(x) é continua em x0=b, e assim determinar quem é b.
Passo 2
Ao substituir x0 = b na função, percebemos que a expressão onde vamos substituir esse valor é a primeira função, pois a mesma está definida para x0 = b. Com isso temos que f ( b ) = b2 -7.
Passo 3
Para verificar que um limite existe devemos lembrar do conceito de limites laterais, ou seja ,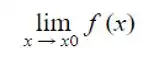 
.
Assim, temos que :
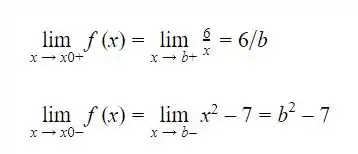
Com isso podemos afimar que para que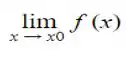 
exista, seus limites laterais devem ser iguais, assim:
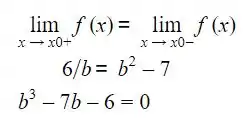
Após resolver a equação cubica acima, encontramos 3 valores para b( b = -1, b = -2 e b = 3). Como o enunciado diz para determinarmos um valor de b, escolheremos b = 3. Logo, para b = 3 podemos afirmar que f é continua.
Resposta
Um valor de b para o qual f(x) é contínua é b = 3.