Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 32
32. Dada , ache se não for inteiro. Prove aplicando o Teorema 3.2.1, que não existe se for inteiro. Se for inteiro, o que poderá ser dito sobre ?
Passo 1
Ao observar o enunciado percebemos que eles nos pede uma série de coisas, basta resolver uma etapa de cada vez utilizando-se de todos os conceitos já vistos nas questões anteriores, bem como de algumas sacadas quanto à afirmações feitas no enunciado.
De início, ele nos pede para encontrarmos a primeira derivada de f em x1, para isso devemos utilizar uma das definições de derivadas.
Após, ele pede para provarmos que a primeira derivada de f em x1 não existe caso x1 seja um número inteiro, para isso utiliza-se do conceito de continuidade de funções.
Por fim, ele pede para analisarmos as derivadas primeira à esquerda e à direita de x1, ou seja , oque poderá ser dito seria como se fizéssemos uma análise em ambas.
Passo 2
Se x1 não é inteiro, então existe um inteiro N tal que N
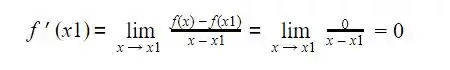
Logo, se x1 não for inteiro temos que 
.
Passo 3
Nota: tome x0 = x1;
Para determinar se f(x) é continua em um ponto deve-se atender a 3 pré-requisitos, ou seja , para uma função ser continua em x0:
f(x0) tem que existir;
-
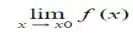tem que existir; -
.
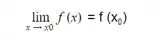Assim, deve-se verificar cada um dos itens ácima para dizer se f(x) é continua em x0.
Passo 4
Sabemos que f ( x1 ) existe, com isso a primeira das condições para que seja contínua é aceita.
Passo 5
Agora, devemos verificar a segunda condição.
Para verificar que um limite existe devemos lembrar do conceito de limites laterais, ou seja ,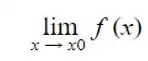 
.
Assim, temos que se x1 for inteiro :
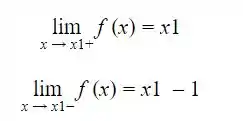
Com isso podemos afimar que 
não existe. Assim, uma das condições para que f seja contínua já não foi aceita. Logo, podemos afirmar que f não é contínua em x1.
Portanto, o teorema 3.2.1 diz que se uma função for derivável em x1 ela é contínua em x1, como descobrimos que f não é contínua em x1 podemos afirmar que f não é derivável em x1, ou seja, 
.
Passo 6
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
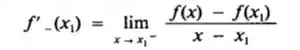
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
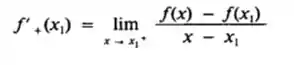
Se x1 for inteiro, temos que
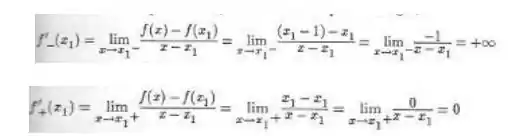
Logo, poderá ser dito que a derivada primeira à esquerda de x1 não existe e que a derivada primeira à direita de x1 é igual a 0. A partir disso também podemos afirmar, se x1 for inteiro, que a derivada primeira em x1 não existe.
Resposta
Demonstração.