Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 36
36. Seja a função definida por
Prove que se existir, será contínua em a.
Passo 1
Como do enunciado ele já me fala que g’(a) existe, tenho que mostrar apenas que f é contínua. Para determinar se f(x) é continua em um ponto deve-se atender a 3 pré-requisitos, ou seja , para uma função ser continua em x0:
- f(x0) tem que existir;
-
.
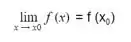tem que existir;
Assim, deve-se verificar cada um dos itens ácima para dizer se f(x) é continua em x0.
Passo 2
Ao substituir x0 = a na função, percebemos que a expressão onde vamos substituir esse valor é a segunda função, pois a mesma está definida para x0 = a. Com isso temos que f ( a ) = g’ (a).
Passo 3
Para verificar que um limite existe devemos lembrar do conceito de limites laterais, ou seja ,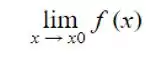 
.
Assim, temos que :
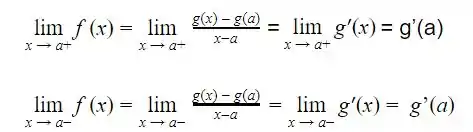
Com isso podemos afimar que 
existe e é igual a g’(a).
Passo 4
Verificando a ultima condição , temos:
Com isso, como os 3 itens necessários foram atendidos; pode-se afirmar que f (x) é continua em x0 = a. Assim, percebemos que se uma função for derivável em x = a, consequentemente, ela é contínua em x = a. Porém, a recíproca não é verdadeira, ou seja , se ela for contínua em x = a nem sempre ela é derivável em x = a.
Resposta
Demonstração.