Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 55
Explique um parágrafo explicando o que significa uma função ser derivável. Inclua exemplos de funções que não sejam deriváveis, bem como exemplos de funções que sejam deriváveis.
Passo 1
Uma função é derivável em , sendo parte do domínio de , se existir , ou seja, se existir derivada nesse ponto.
Geometricamente falando, uma função é diferenciável em se o gráfico de possuir uma reta tangente em .
Passo 2
Como uma função não derivável podemos citar:
Veja o gráfico da função abaixo:
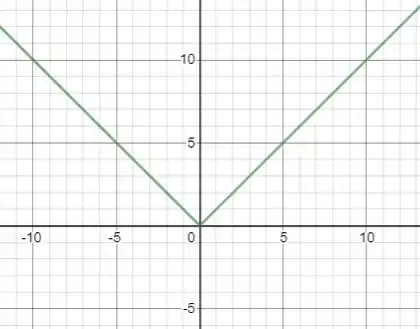
Ela é contínua em , pois existe , porém não é diferenciável nesse ponto, pois aí temos um bico, não podemos encontrar uma reta tangente nesse ponto.
Passo 3
Já um exemplo de funções que sejam deriváveis temos:
Vamos ver o gráfico da função abaixo:
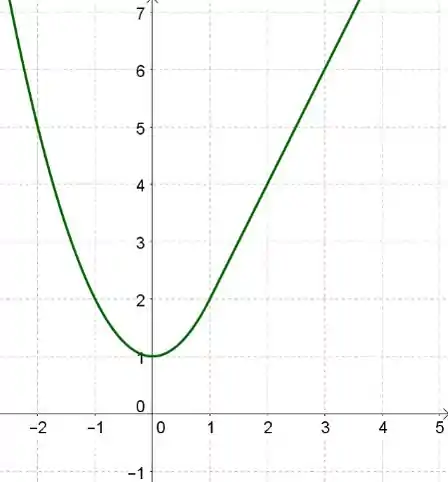
Vamos agora provar que é diferenciável, vamos calcular o limite no ponto tanto pela direita quanto pela esquerda, e os dois valores devem ser iguais para ela ser diferenciável:
Vamos então aplicar para direita:
Agora vamos manipular o limite:
E por último vamos cancelar o termo do numerador e do denominador e vamos aplicar o limite:
Passo 4
Agora vamos aplicar para esquerda:
Agora vamos manipular o limite:
E por último vamos cancelar o termo do numerador e do denominador e vamos aplicar o limite:
Assim temos que , então a função é diferenciável.
Resposta
Ei, a resposta está no passo a passo :)