Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 23

Dada a equação vetorial

r   u , v = u cos ⁡ v ,       u   s e n   v ,     u ²

b) fazer esboço e indicar o significado geométrico dos parâmetros u e v

c) determinar a área da parte da superfície que esta entre os planos z = 0 e z = 4

Passo 1

b)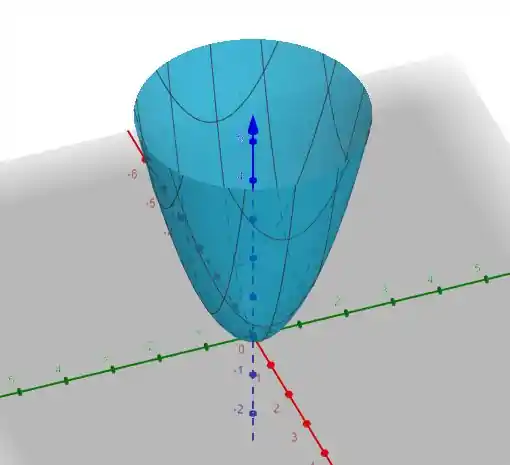

Quando temos uma equação parametrica temos que perceber o movimento da nossa função

O paramentro v esta nas funções seno e cosseno logo ele é responsavel pelo movimento circular.

Ao passo como u esta multiplicando o seno e cosseno ele funcina como raio. Então conforme nosso u cresce, vamos vendo circulos cada vez maiores em z. Isso forma um paraboloide.

Passo 2

c) Bem ao queremos calcular uma integral de superfície existe algumas maneiras. A exposta nessa seção é a seguinte

∫ ∫ R ∂ r ∂ u   x ∂ r ∂ v   d u d v

A primeira coisa é achar nossos limites de integração. Sabemos pelo enunciado que nosso paraboloide vai de z = 0 a z = 4. E como nossa função é parametrizada vamos precisar ser sagazes agora

r   u , v = u cos ⁡ v ,       u   s e n   v ,     u ²

A função que define o comportamento em z é u ² . Assim quando

z = 0 → u = 0

e

z = 4 → u = 2

Logo nossos limites são u ∈ [ 0,2 ] e v ∈ [ 0,2 π ]

Passo 3

Agora vamos achar as derivamos parciais de r

∂ r ∂ u =   ∂ ∂ u u cos ⁡ v ,       u   s e n   v ,     u ²

= cos ⁡ v ,     s e n v ,     2 u

E também

∂ r ∂ v =   ∂ ∂ v u cos ⁡ v ,       u   s e n   v ,     u ²

= - u s e n   v ,     u c o s v   ,     0

Agora vamos fazer o rotacional das derivadas parciais

∂ r ∂ u   x ∂ r ∂ v =   x → y → z → cos ⁡ v s e n   v 2 u - u   s e n   v u cos ⁡ v 0

Assim o determinante dessa matriz é

∂ r ∂ u   x ∂ r ∂ v = - 2 u 2 cos ⁡ v   ,   - 2 u 2 s e n v   ,       u  

Então se voltarmos a nossa integração fica

∫ 0 2 π ∫ 0 2 - 2 u 2 cos ⁡ v   ,   2 u 2 s e n v   ,       u     d u d v

So lembrando que o modulo é aplicar raiz quadrada em cima de todos os termos elevados ao quadrado. (É como se estivéssemos fazendo a relação de Pitágoras com as compenetres 😊)

∫ 0 2 π ∫ 0 2 - 2 u 2 cos ⁡ v ) ²   +     ( 2 u 2 s e n v ) ²     +   (   u 2   d u d v

Temos como simplificar nossa vida com a relação trigonométrica básica

∫ 0 2 π ∫ 0 2 4 u 4 + u 2   d u d v

Vamos integrar em V primeiro já que nossa integral não depende de v

2 π ∫ 0 2 4 u 4 + u 2   d u

= 2 π ∫ 0 2 u 4 u 2 + 1   d u

= 2 π 8 * 2 3   4 u 2 + 1 3 2 0 2

= 3 π 2 9 3 / 2 - 1

= 3 π 2 26

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ ∫ R ∂ r ∂ u   x ∂ r ∂ v   d u d v = 39 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície S é formada pelo cilindro x 2 + y 2 = 1 ,- 1 ≤ z ≤ 1 , e por círculos no fundo e no topo. Suponha que você saiba que f é uma função contínua com f ± 1,0 , 0 = 2 , f 0 , ± 1,0 = 3 e f 0,
Seja S o cubo com vértices ± 1 , ± 1 , ± 1 . Aproxime ∫ ∫ S x 2 + 2 y 2 + 3 z 2d S usando as somas de Riemann como na Definição 1, tomando os retalhos S i j como os quadrados que são as faces do cubo
Encontrar a área da superfície do plano 2 x + y + 2 z = 16 , interceptado por x = 0 ,y = 0 ,x = 2 e y = 3 x = 0 ,y = 0 e x 2 + y 2 = 36 , no 1° octante
Calcular a área da superfície do paraboloide y = 3 - ( x 2 + z 2 ) interceptado pelo plano y = 0
Calcular a área da superfície plana 2 x + 2 y + 3 z = 6 , tomada no 1 ° octante.