Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 63
Dada
(a) Faça um esboço do gráfico de f. (b) Determine se f é contínua em 3. (c) determine se f é derivável em 3.
Passo 1
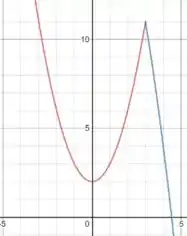
Para a letra (a) o gráfico abaixo mostra em vermelho a primeira parte da função para e em azul para
Passo 2
Para a letra (b), vamos analisar se a função é contínua em 3, primeiro fazemos x tender a 3 pela esquerda:
Agora pela direita:
E então resolvemos a função quando :
Como todas deram o mesmo resultado, a função é contínua em 3.
Passo 3
Na letra (c) precisamos mostrar que a função é derivável em 3, para isso, aplicamos a definição de derivada com x tendendo a 3 pela esquerda e pela direita:
Simplificando:
Aplicando o limite:
Fazendo agora pela direita:
Como os resultados são diferentes, f não é derivável em 3.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
37. O gráfico de 𝑔 é dado. (a) Em quais números g é descontínua? Por quê? ( b ) Em quais números g não é diferenciável? Por quê?
37. O gráfico de f é dado. Estabeleça, explicando, os números nos quais f não é diferenciável.
Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.