Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 11
a) Esboce o gráfico de uma função que tenha um máximo local em e seja derivável em .
b) Esboce o gráfico de uma função que tenha um máximo local em e seja contínua, mas não derivável em .
c) Esboce o gráfico de uma função que tenha um máximo local em e não seja contínua em .
Passo 1
Esta é uma questão muito interessante para verificar se o aluno consegue perceber a diferença entre continuidade e diferenciabilidade graficamente e, além disso, como estas coisas se relacionam com pontos de extremos.
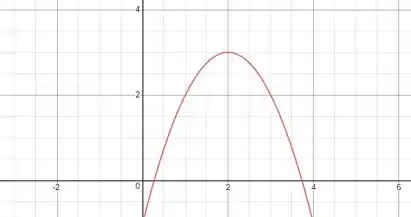
No item (a), devemos esboçar o gráfico de uma função que tenha um máximo local e seja derivável em . Como a função deve ser derivável, ela também deve ser contínua nessa ponto. Basta traçar uma curva suave que possa ter reta tangente em e, além disso, que seja máximo local nessa ponto. A forma mais fácil de se fazer isso é traçando uma curva com concavidade para baixo e que tenha tangente horizontal em :
Passo 2
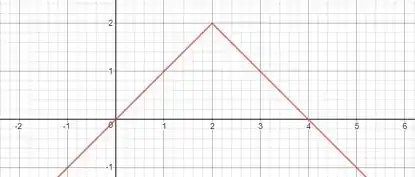
Agora queremos uma função que seja contínua, mas não derivável em . Para isso, basta introduzir um bico neste ponto:
Passo 3
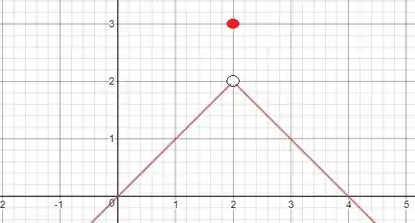
Por fim, queremos um gráfico de uma função que não seja contínua em mas tenha máximo local nesse ponto. A forma mais fácil de se fazer isso é introduzir uma descontinuidade removível nesse ponto:
Prontinho!
Resposta
Esboço de gráfico.