Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 5
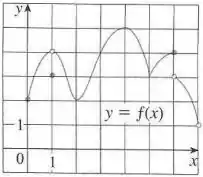
Use o gráfico para dizer quais os valores máximos e mínimos locais e absolutos da função.
Passo 1
Opa! Bora pra mais uma questão!? Nesse enunciado é dado o gráfico de uma função e devemos primeiro localizar os extremos (locais e globais) e, em seguida, fornecer os valores da função nestes pontos.
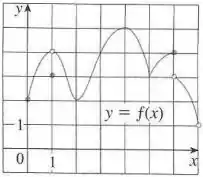
Para isso a gente vai analisar o gráfico e encontrar os pontos onde a função deixa de ser crescente e passa a ser decrescente e vice e versa. Esses serão os máximos e mínimos locais respectivamente.
O máximo e mínimo não tem erro, a gente precisa identificar o maior e menor valor possível da função, respectivamente!
Passo 2
Vamos primeiro identificar os pontos de máximo e mínimo locais.
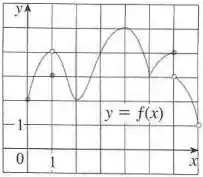
Para achar os mínimos locais olhamos os pontos onde a curva deixa de ser decrescente e passa a ser crescente, dessa forma temos os pontos , e .
Nos máximos locais é o contrário, a função deixa de ser crescente e passa a ser decrescente, portanto temos os pontos e .
Note que o ponto aparenta ser um máximo local, com , porém como temos uma bolinha aberta o valor real é na realidade , que é um valor menor que o o valor da função na vizinhança de .
Passo 3
O máximo global é o maior valor da função, ele ocorre em e a função não tem mínimo global devido a bolinha aberta em .
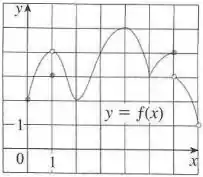
Nesse caso não temos um mínimo local, já que tem a bolinha aberta.
Resposta
Mínimo local: , e .
Máximo local:
Mínimo absoluto: não tem.
Máximo absoluto: .