Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 26
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Oiee bora resolver essa comigo?
Vamos esboçar o gráfico da função
E encontrar os valores máximos e mínimos locais e absolutos.
- Domínio: A fun��ão está definida para todos os valores reais de
- Intercepto y: A função cruza o eixo y em Então,
- Comportamento Assintótico:
- À medida que
- À medida que
Passo 2
A derivada de é:
- Como para todos os a função é sempre crescente.
- Não há pontos críticos onde a derivada seja zero ou indefinida, pois para qualquer
- Máximo Absoluto: Como é sempre crescente e não tem um valor máximo finito, não há máximo absoluto.
- Mínimo Absoluto: O valor mínimo absoluto ocorre quando No entanto, como tende a mas nunca chega a , o mínimo absoluto é mas não é atingido em nenhum ponto finito de
Passo 3
Vamos esboçar o gráfico da função
1. Para
2. Para
3. Para
4. À medida que
5. À medida que
Passo 4
Esboço do gráfico
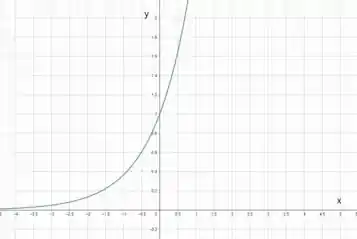
- Máximo Absoluto: Não há máximo absoluto porque a função cresce indefinidamente à medida que aumenta.
- Mínimo Absoluto: O mínimo absoluto ocorre no limite quando e é
A função é uma função exponencial crescente sem valores máximos locais ou absolutos finitos, mas com um mínimo absoluto de que é alcançado no limite.
Resposta
Vide o passo a passo.