Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 35
35. Dada . Onde a é um inteiro, mostre que .
Passo 1
Nesta questão ele nos pede para mostrar que a derivada à esquerda + 1 é igual derivada à direita de f (x) em x1 = a.
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
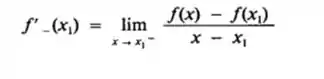
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
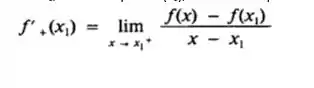
Passo 2
A derivada à esquerda de f(X) em x1 = a será:
Passo 3
A derivada à direita de f(X) em x1 = a será :
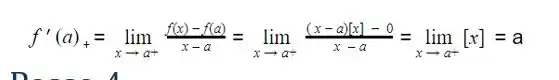
Passo 4
Assim ,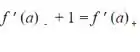 
.
Resposta
Demonstração.
Exercícios de Livros Relacionados
O gráfico de f é dado. Diga, explicando quais, os números em que f não é diferenciável
O gráfico de f é dado. Diga, explicando quais, os números em que f não é diferenciável
O gráfico de f é dado. Diga, explicando quais, os números em que f não é diferenciável
Suponha que uma função f seja diferenciável em x 0 . Modifique o argumento do Exercício 53 para provar que a reta tangente ao gráfico de f no ponto P x 0 , f x 0 fornece a melhor aproximação linear de
Suponha que uma função f seja diferenciável em x = 0 com f 0 = f ' 0 = 0 , e seja y = m x , m ≠ 0 , uma reta pela origem de inclinação não nula.Prove que existe um intervalo aberto contendo 0 , tal qu