Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 40
O gráfico de é dado. Diga, explicando quais, os números em que não é diferenciável
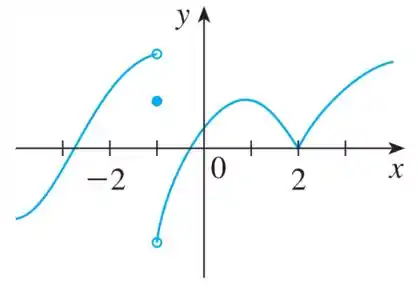
Passo 1
Fala aí! tudo certinho? 😊
Nesse problema temos um gráfico de uma função
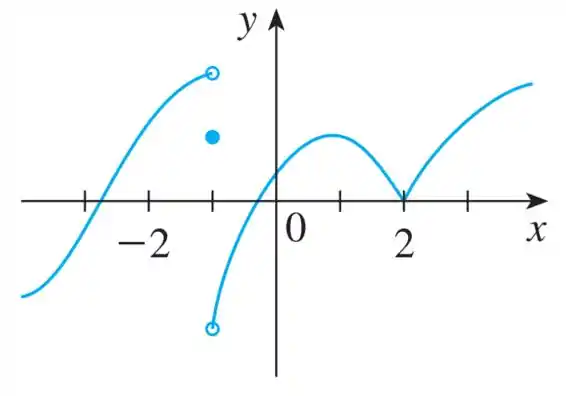
e nosso objetivo é determinar os pontos onde a função não é diferenciável.
Tem ideia de como fazemos isso? 🤔
Existem algumas características nos gráficos das funções que podem indicar onde a função não é diferenciável:
Descontinuidades: Se houver descontinuidades no gráfico da função, a função não será diferenciável nessas regiões. Isso inclui descontinuidades em pontos isolados, descontinuidades infinitas e descontinuidades removíveis.
Pontos angulares: Pontos onde a tangente à curva tem uma mudança brusca de direção indicam falta de diferenciabilidade. Isso geralmente ocorre em pontos onde a função tem um canto afiado.
Picos e vales afiados: Se houver picos ou vales muito agudos no gráfico da função, esses pontos podem indicar falta de diferenciabilidade, especialmente se a função muda rapidamente em torno desses pontos.
Pontos de inflexão: Embora os pontos de inflexão indiquem onde a concavidade da função muda, eles podem não indicar necessariamente falta de diferenciabilidade. No entanto, eles podem ocorrer em pontos onde a função não é diferenciável, então é importante verificar.
Gráficos irregulares ou "pulverizados": Às vezes, as funções podem ter gráficos muito irregulares, com comportamento oscilatório ou altamente fragmentado. Nessas situações, é necessário analisar cuidadosamente para determinar se a função é diferenciável em todos os pontos.
Veja só! 👀
Passo 2
Uma função não é diferenciável nos pontos onde ela forma uma “ponta” e nos pontos de descontinuidade.
O gráfico da função é dado por
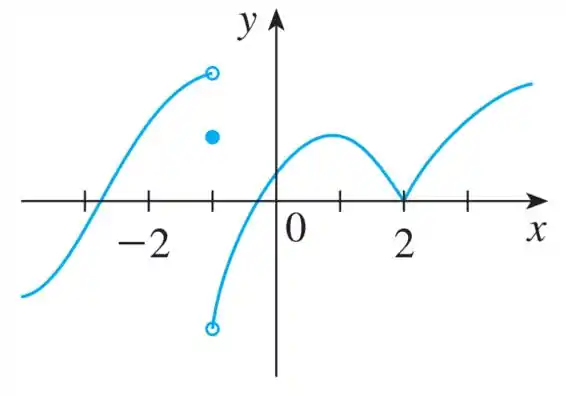
A função dada não é diferenciável nos seguintes pontos:
- em devido à descontinuidade de salto (a função deve ser contínua para ser diferenciável em um ponto). Aqui temos limites laterais diferentes e o valor da função em si é dada por outro ponto.
- em devido ao gráfico não ser suave naquele ponto, há um recorte/borda acentuada.
E aí! o que achou? Responde Aí! 😉