Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 41
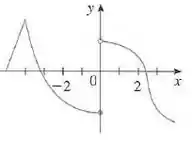
O gráfico de é dado. Diga, explicando quais, os números em que não é diferenciável
Passo 1
Fala aí! tudo certinho? 😊
Nesse problema temos um gráfico de uma função
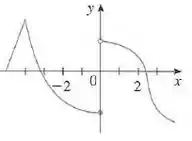
e nosso objetivo é determinar os pontos onde a função não é diferençável.
Tem ideia de como fazemos isso? 🤔
Existem algumas características nos gráficos das funções que podem indicar onde a função não é diferenciável:
Descontinuidades: Se houver descontinuidades no gráfico da função, a função não será diferenciável nessas regiões. Isso inclui descontinuidades em pontos isolados, descontinuidades infinitas e descontinuidades removíveis.
Pontos angulares: Pontos onde a tangente à curva tem uma mudança brusca de direção indicam falta de diferenciabilidade. Isso geralmente ocorre em pontos onde a função tem um canto afiado.
Picos e vales afiados: Se houver picos ou vales muito agudos no gráfico da função, esses pontos podem indicar falta de diferenciabilidade, especialmente se a função muda rapidamente em torno desses pontos.
Veja só! 👀
Passo 2
O gráfico da função é dado por
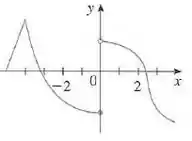
Portanto, pelo gráfico, não é diferenciável nos pontos:
Onde temos uma “ponta” em e uma descontinuidade em , onde os limites laterais da função são diferentes.
E aí! o que achou? Responde Aí! 😉