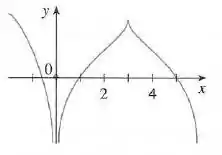
O gráfico de é dado. Diga, explicando quais, os números em que não é diferenciável

Olá, meu amigo. Tudo bem? Espero que você esteja pronto e animado para darmos início a mais uma resolução.

Aqui a gente tem um gráfico de uma função, e nos é perguntando em quais pontos a função não é diferenciável.

Para identificar os pontos onde uma função não é diferenciável apenas observando seu gráfico, você precisa procurar por características específicas que indicam falta de continuidade ou comportamento irregular, como mostrados e explicados abaixo:

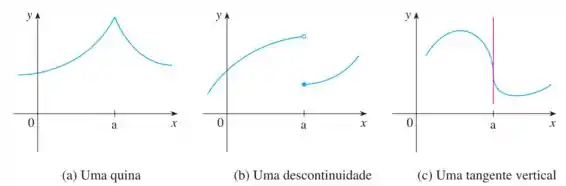
Descontinuidades: Pontos onde a função não é contínua indicam falta de diferenciabilidade nesse ponto.

Pontos angulosos (Cúspides): Em alguns pontos, a função pode formar uma cúspide ou uma espécie de "ponta" no gráfico. Isso geralmente ocorre quando há uma mudança súbita na direção da curva.

Pontos de quebra (Ligação de Tângentes): Em alguns casos, a função pode mudar de uma tangente para outra de forma abrupta. Isso indica falta de suavidade na função e, portanto, falta de diferenciabilidade nesse ponto.

Picos ou vales acentuados: Se a função tem picos ou vales muito íngremes, isso pode indicar que a função não é diferenciável nesses pontos, especialmente se a inclinação muda abruptamente.

Pontos de tangência vertical: Quando a inclinação da função é vertical em algum ponto, a função não é diferenciável nesse ponto.

Assíntotas verticais: Se a função se aproxima de uma linha vertical sem nunca cruzá-la, pode indicar uma falta de diferenciabilidade naquele ponto.