Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 25a
25. Dada . (a) Prove que não existem. (b) Prove que . (c) Faça um esboço do gráfico de
Letra ( a )
Passo 1
Antes de mais nada devemos saber que sgn x é igual a função sinal. Em matemática e informática, a função sinal é a função que retorna o sinal do número real. Ou seja :
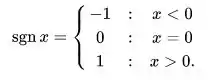
O que o enunciado nos pede nesta letra é para mostrarmos que em x1 = 0 nem a derivada à direita nem a derivada à esquerda de f(x) existem. A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
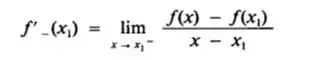
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
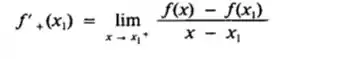
Passo 2
A derivada à direita de f(X) em x1 = 0 será :
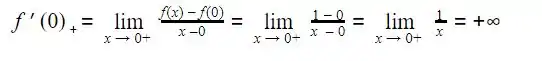
Passo 3
A derivada à esquerda de f(X) em x1 = 0 será :
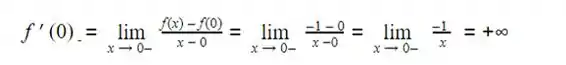
Logo, 
.
Resposta
Demonstração.
Exercícios de Livros Relacionados
Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
Calcular a diferencial das seguintes funções:(a) y = ln ( 3 x 2 - 4 x ) ;(b) y = x + 1 e x ;(c) y = sin ( 5 x 2 + 6 )
Calcular um valor aproximado para as seguintes raízes, usando diferencial.(a) 50 ;(b) 63,5 3 ;(c) 13 4
Calcular um valor aproximado para as seguintes raízes, usando diferencial.(a) 50 ;(b) 63,5 3 ;(c) 13 4