Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 2
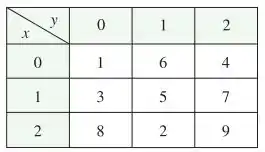
É dada uma tabela de valores de uma função com gradiente contínuo. Determine , onde tem equações paramétricas:
Passo 1
Antes de qualquer coisa, vamos transformar essas equações paramétricas em uma função vetorial ou , tudo bem? Temos:
Mas para determinarmos a integral de linha temos que saber quanto vale , logo:
Como os valores de estão definidos em , isso implica que , então pelo teorema , segundo o Stewart, temos:
Passo 2
De acordo com o que nos foi dado, temos que o ponto inicial é em , logo:
Sendo assim:
Olhando na tabela que a questão nos fornece, e resulta em , então:
De acordo com o que nos foi dado, temos que o ponto final é em , logo:
Sendo assim:
Olhando na tabela que a questão nos fornece, e resulta em , então:
Passo 3
Agora que descobrimos os valores finais e iniciais que queríamos, basta utilizarmos a expressão do passo 1, se liga:
E é esse o nosso resultado!