Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.3 - Ex. 23
O campo vetorial é conservativo? Explique.
Passo 1
E aí, tudo bem?
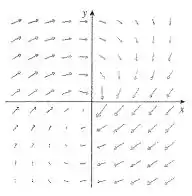
Basicamente o que a questão está pedindo é que olhemos para a figura
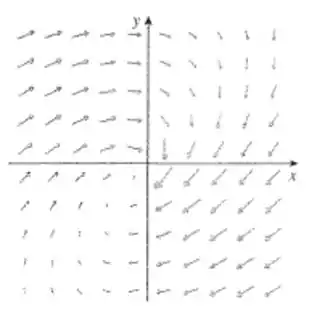
E digamos se esse campo é conservativo ou não. E para um campo ser conservativo, o rotacional tem que ser .
Ok, mas como identificamos isso?
De um jeito simples, para que um campo seja conservativo, ele não pode aparentar estar girando em torno de algum ponto.
Partiu analisar a figura?
Passo 2
Olhando para a figura
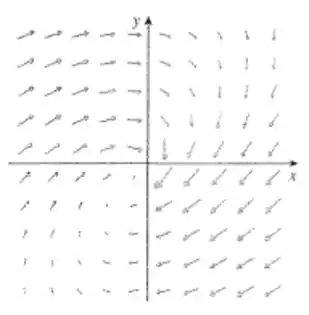
Podemos perceber claramente que o campo está girando em torno do centro, então, claramente esse campo possui algum rotacional.
Sendo assim, o campo não é conservativo!
Outro jeito de analisar seria:
Desenhar várias curvas fechadas. A partir desse desenho, a gente começa a analisar se os vetores estão na mesma direção ou não que o nosso caminho.
Basta desenhar uma circunferência centrada na origem.
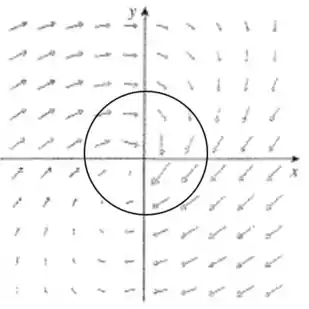
Vocês vão perceber que os vetores estão predominantemente no mesmo sentido do caminho (ou no sentido contrário). Por causa disto, o campo não é conservativo!
Resposta
O campo não é conservativo.