Dadas as tabelas a seguir, encontre as derivadas indicadas em (a) e (b).
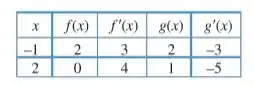
a) , onde
b) , onde
Passo 1
Meus queridos e minhas queridas!
Sabemos que, pela regra da cadeia:
Logo, para responder a letra a):
Passo 2
Para responder a letra b):
Dadas as tabelas a seguir, encontre as derivadas indicadas em (a) e (b).

a) , onde
b) , onde
Meus queridos e minhas queridas!
Sabemos que, pela regra da cadeia:
Logo, para responder a letra a):
Para responder a letra b):